A. head
Hausarbeit im Fach AVL, Modul “Vergleichende Literaturgeschichte”.
Seminar: “DIE SCHÖNSTEN LENGEVITCHES: DYNAMIKEN DER POST-DEUTSCHEN GEGENWARTSLYRIK”.
Dozentin: Chiara Liso.
SoSe 2022.
eingereicht: 2022-12-30
edited: 2023-01-01
anderes format: view .pdf
einleitung
Wir werden im Folgenden den Versuch unternehmen, aus einigen statistischen Berechnungen Aussagen zum lyrischen Werk Uljana Wolfs abzuleiten. Ob daraus Erkenntnisse hinsichtlich des Aspekts postdeutsch erwachsen, können wir noch nicht sagen.
Die Arbeit wird explorativ vorgehen, dh. unser Erkenntnisinteresse ist durchaus ungerichtet. Wir wollen wesentlich einige Methoden zur Anwendung bringen, die geeignet erscheinen, weitere literaturwissenschaftliche Fragestellungen zu beantworten. Eine weiter gefasste Aufgabenstellung dieser Arbeit würde ca. lauten:
task
Bestimmung charakteristischer Merkmale im lyrischen Werk Uljana Wolfs mithilfe statistischer Methoden.
zur autorin
Uljana Wolf, der Öffentlichkeit seit 2005 durch ihre Gedichte bekannt, wurde 2006 für ihr Debüt kochanie ich habe brot gekauft (kookbooks 2005) mit dem Peter-Huchel-Preis ausgezeichnet und veröffentlichte seitdem neben Übersetzungen und essayistischen Schriften zwei weitere Gedichtbände, ebenfalls bei kookbooks. Dort ist sie in ein enges Netzwerk junger deutschsprachiger Autor:innen eingebunden, die sich auch (hier zum Aspekt postdeutsch) mehrheitlich durch ihre Affinität zu mehr- oder polylingualer Dichtung auszeichnen. Es gibt bei kook kaum Dichter:innen, deren Werk nicht irgendwie Mehrsprachigkeit künstlerisch ausdrückt, damit arbeitet. Nicht alle vereint eine wirklich (muttersprachliche Provenienz) in anderen europäischen u.a. Sprachen als dem Deutschen, die meisten jedoch deren unmittelbarer Einflusz auf ihre Dichtung. Uljana Wolf hält dazu in ihrem Aufsatz ZU MEHRSPRACHIGKEIT IM GEDICHT fest, dasz Mehrsprachigkeit “ein ästhetisches, kein biografisches Moment” sei und “dass auch von einsprachigen oder einmuttersprachigen Autor:innen translinguale Literatur durch verschiedene Schreibstrategien erzeugt werden kann, um festgefügte Sprachordnungen zu verunsichern.” (Wolf 2021, 118). Wolf kommt nicht - sie meint, ihres kochanie wegen vielfach vermutet (Wolf 2021, 5) - aus dem polnisch-ukrainischen Grenzland, sondern aus Ostberlin, hat jedoch intensiv russisch und eben auch polnisch gelernt (und gelebt) und sich in alle Sprachen begeben, die für sie fruchtbar waren; zahlreiche Stipendienaufenthalte und nicht zuletzt ihr zwischen New York und Berlin pendelndes Arbeitswesen zeugen davon.
work
corpus aufbereitung
Das Korpus, welches nach Digitalisierung der Buchvorlagen aus einer Datenbank abgerufen wird, enthält 144 Einträge, nach Abzug der Kapitelüberschriften und Zitate 130 Datensätze (Texte), die zur Auswertung herangezogen werden können.
Für die Analyse wurde das gesamte (publizierte) lyrische Werk Uljana Wolfs, bestehend aus, in der Reihenfolge des Erscheinens:
- kochanie, ich habe Brot gekauft (Wolf 2005)
- falsche freunde (Wolf 2009)
- meine schönste lengevitch (Wolf 2013)
herangezogen.
basic statistics
Wir werden versuchen, in der Arbeit einige Kennzahlen zu bestimmen, die charakteristisch für das Werk sein sollen. Basis sind hier Statistiken über Wortlängen und -frequenzen, Distribution multilingualer Elemente über das Korpus und Annäherungswerte zur Bestimmung des sentiment. Die Zahlen werden absolut und/oder relativ angegeben; absolut meint hier die konkrete Beziehung zu einer Position im Korpus, relativ meint jeweils die indexikalisierte, auf einer Gesamtheit v.H. angenommene Position oder Relation. Diese Relativierung ermöglicht eine gleichförmige Visualisierung der Daten in glatten Frequenzkurven, um die Verhältnisse schematisch abzubilden. (Zur Berechnung der Fourier-transformierten (FFT) Frequenzen cf. Jockers (2015))
ground truth
Die 130 Texte (Lyrik und lyrische oder experimentelle Prosa) haben einen Umfang von 10434 Wörtern (tokens), die sich in 3976 distinct types einteilen lassen, die type/token ratio, ein Indikator für lexical diversity, beträgt demnach 0.3810619. Die durchschnittliche Textlänge (median) beträgt 69 Wörter. Wir haben noch keine Vergleichswerte, die sinnvoll wären…
multiLX
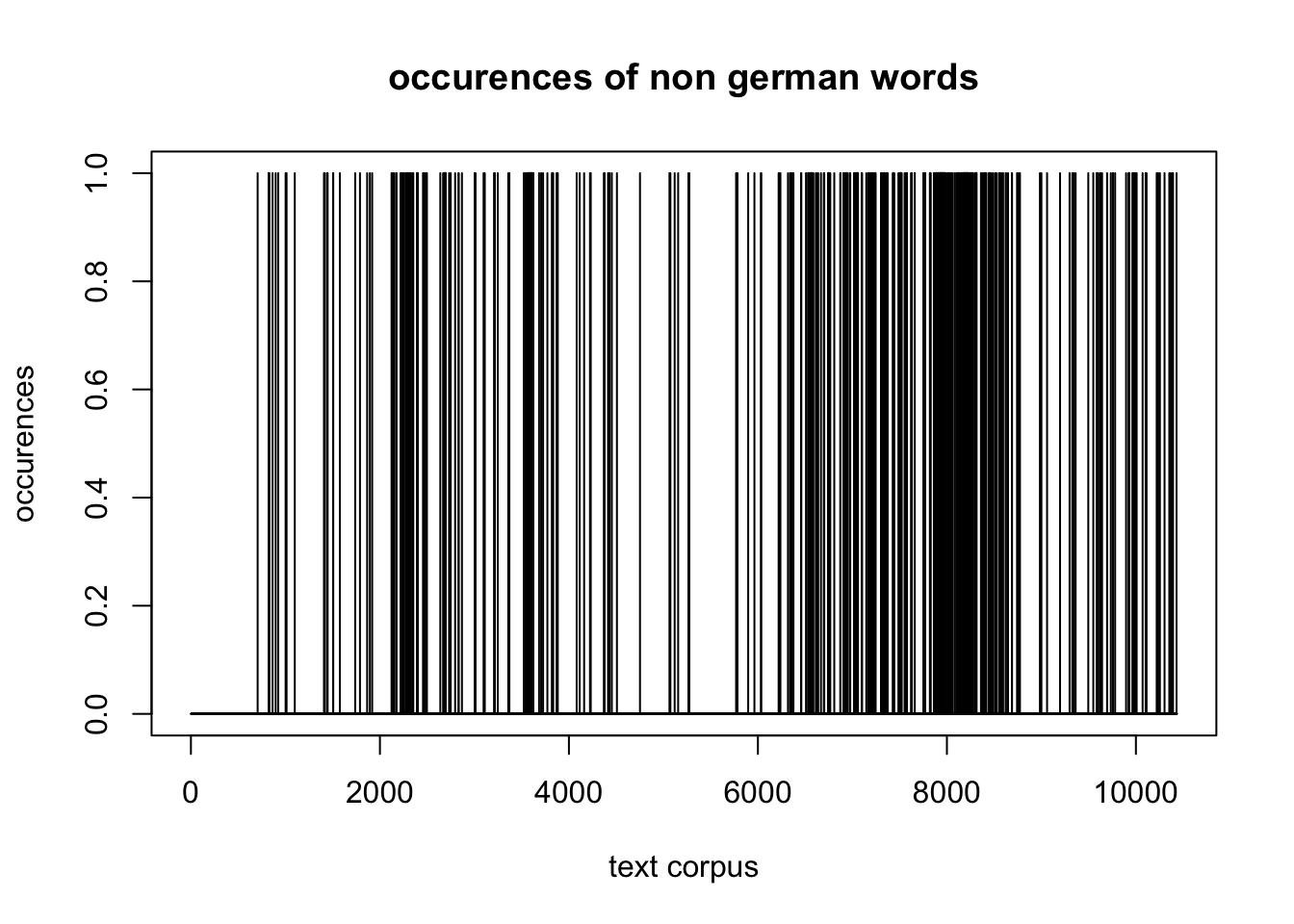
Die multilingualen Elemente des Korpus (insgesamt 700 tokens) haben einen Anteil von 9% an den types.
Mit der Textmatrix (cf. Table 1) läszt sich noch weiter rechnen.
similarities
Table 1: simplest matrix of text beginnings
| gegen |
vier |
uhr |
morgens |
beobachte |
ich |
die |
verschiebung |
| ach |
wär |
ich |
nur |
im |
aufwachraum |
geblieben |
traumverloren |
| ach |
wär |
ich |
nie |
im |
aufwachraum |
gewesen |
taub |
| schließ |
mich |
ein |
liebe |
ins |
gebet |
in |
die |
| diese |
kästen |
enthalten |
frauen |
die |
nicht |
bearbeitet |
werden |
| meine |
väter |
sind |
einfache |
männer |
sie |
haben |
töchter |
| meine |
väter |
sind |
keine |
einfachen |
männer |
sie |
haben |
| meine |
münder |
sind |
keine |
einfachen |
väter |
der |
erste |
| meine |
väter |
sind |
einfache |
vermesser |
der |
erste |
geht |
| meine |
väter |
sind |
keine |
einfachen |
vermesser |
der |
erste |
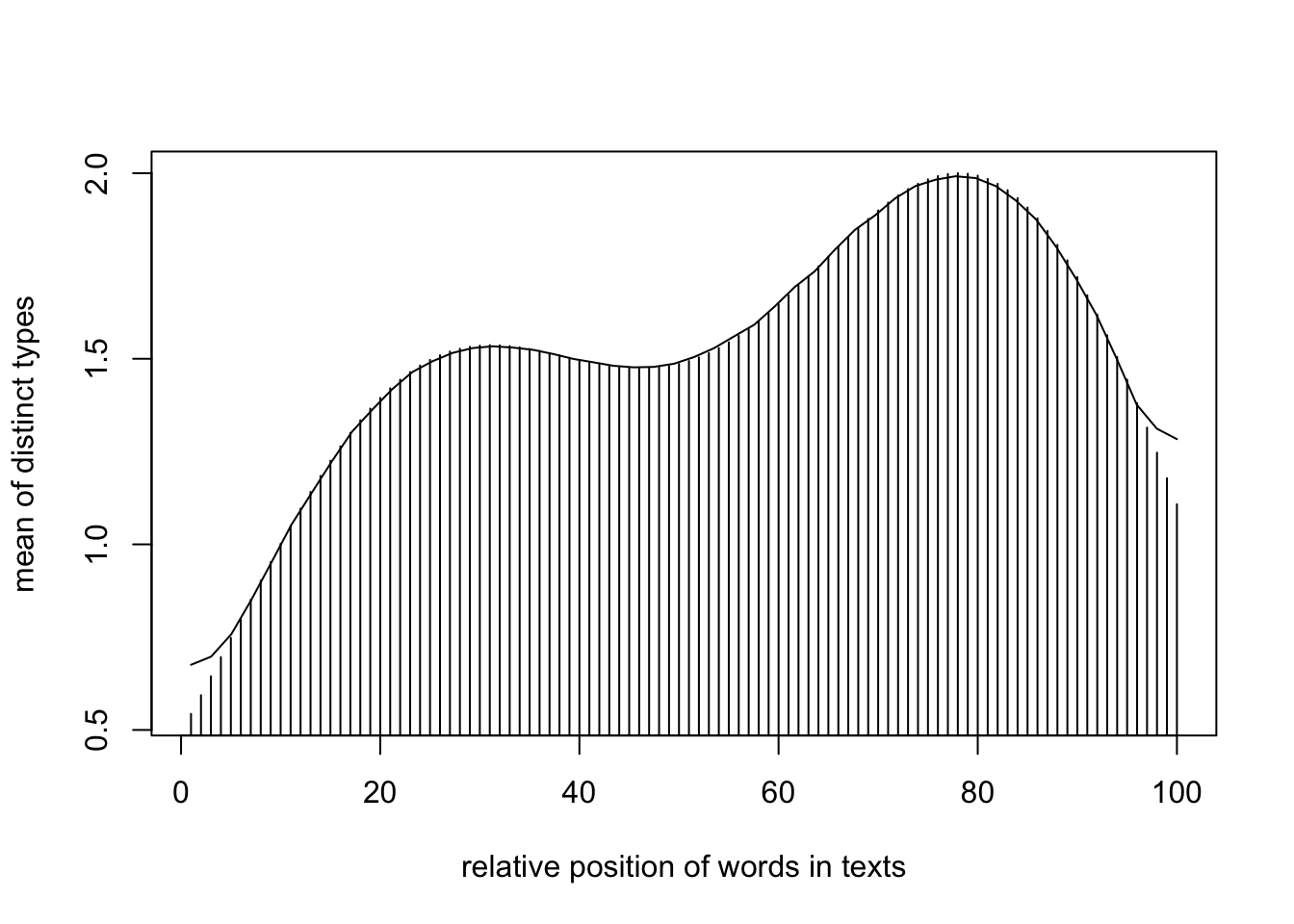
Zum Beispiel lassen sich die Wortgleichungen visualisieren, die an bestimmten Positionen des Textes aufscheinen. Die Höhen in der folgenden Graphik markieren relative (Fourier-transformierte) Wortpositionen, an denen von Wolf die wenigsten analogen Wörter verwendet wurden. Es läszt sich erkennen, dasz ein Text meist mit denselben Wörtern anfängt (baisse), die immer verschiedener werden, um sich bei der Hälfte des Textes über eine lange Strecke zu gleichen und ab 60% sprunghaft zu divergieren bis sie um 78% einen peak (hausse) erreichen an Verschiedenheit.
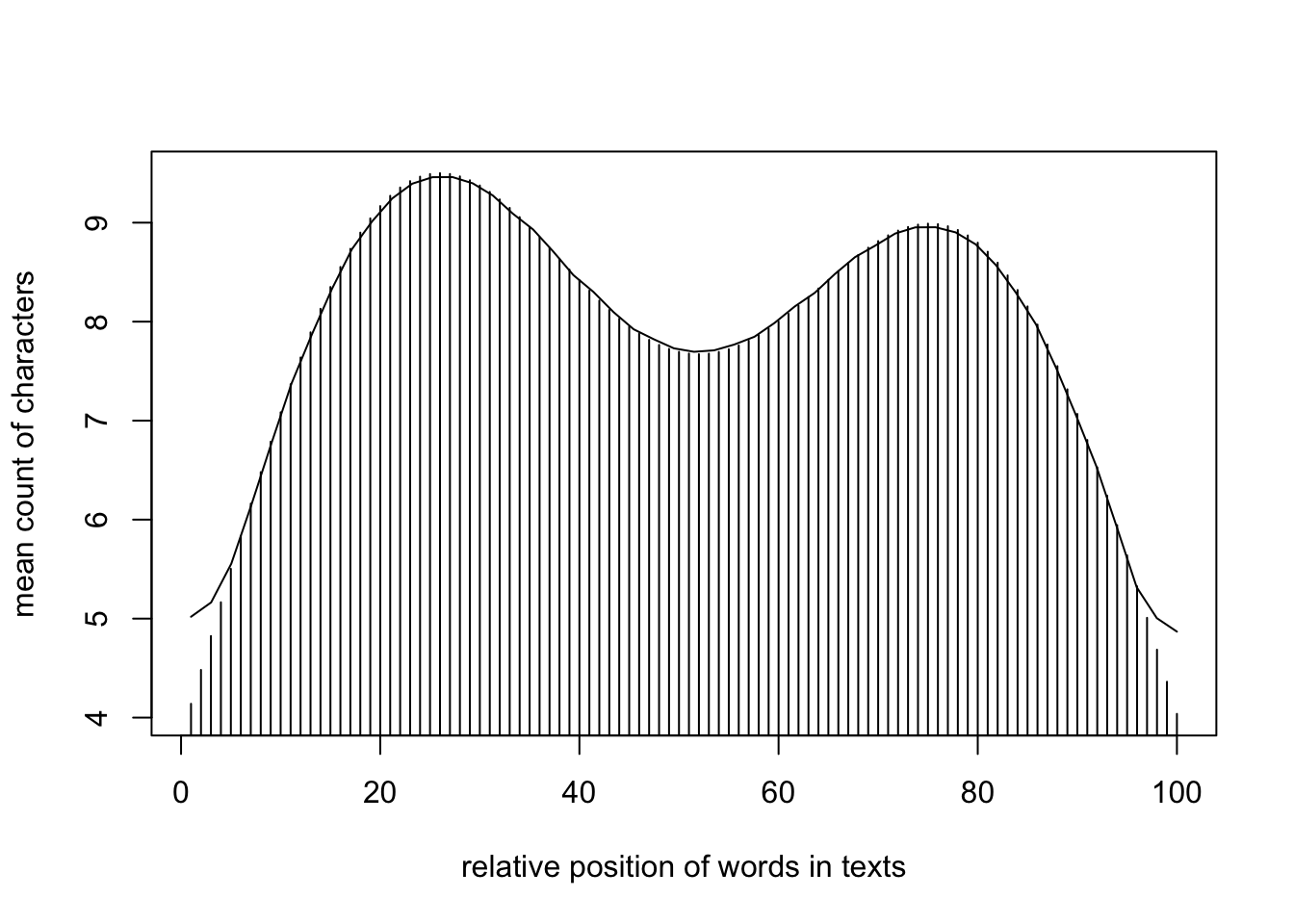
Eine weiterhin schöne Graphik entsteht, wenn man die Matrix der Zeichenanzahl über die Gesamtheit der Wörter visualisiert. Hier zeigt sich, dasz ein Text zwischen 21-31% die längsten Wörter (mean: 9.5 characters) enthält, diese zwischen 36 und 56% kürzer werden bishin zu 7.76 Zeichen um bei 76% einen erneuten peak in der Zeichenanzahl (mean: 8.98 characters) zu erreichen.
sentiment analysis
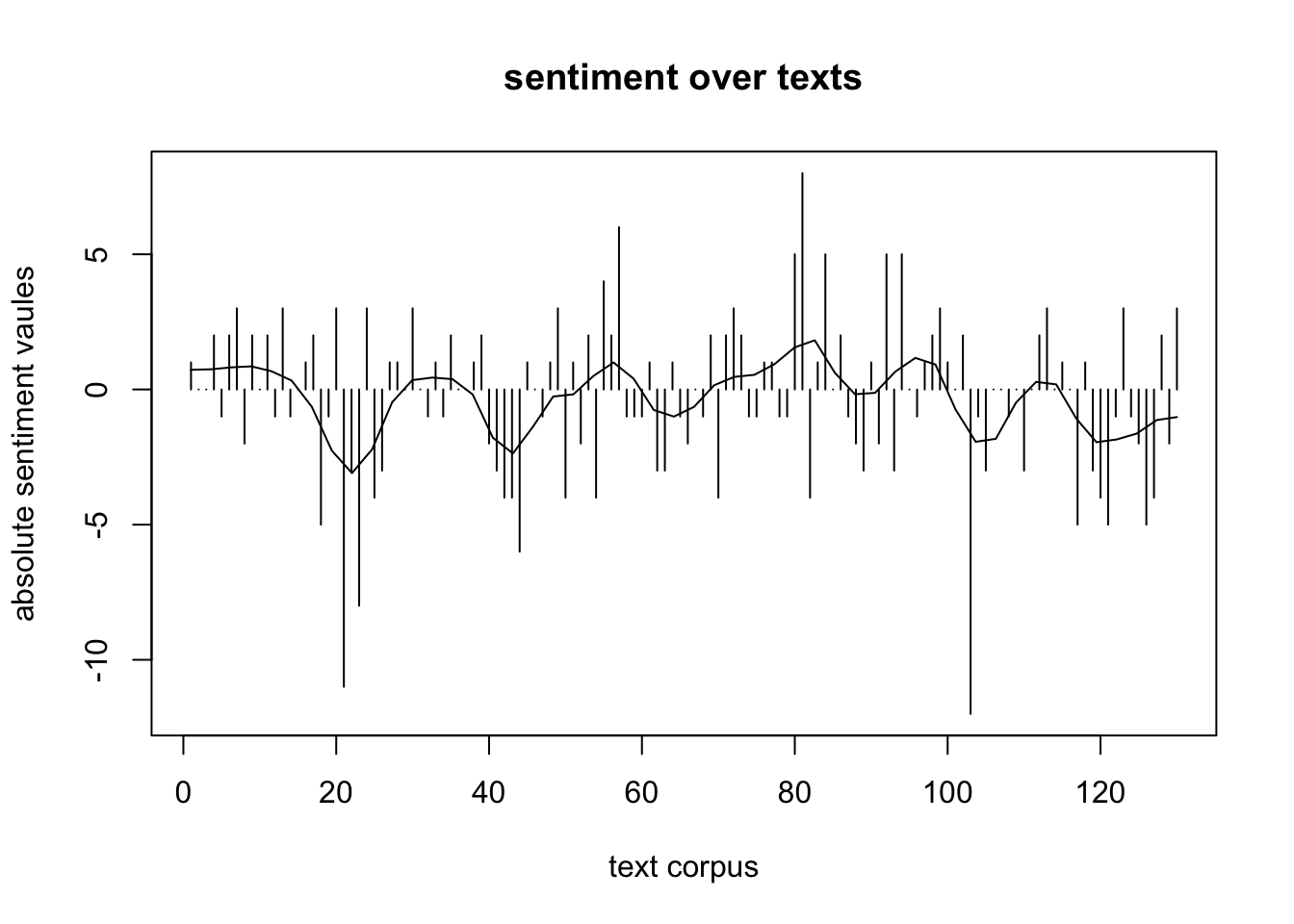
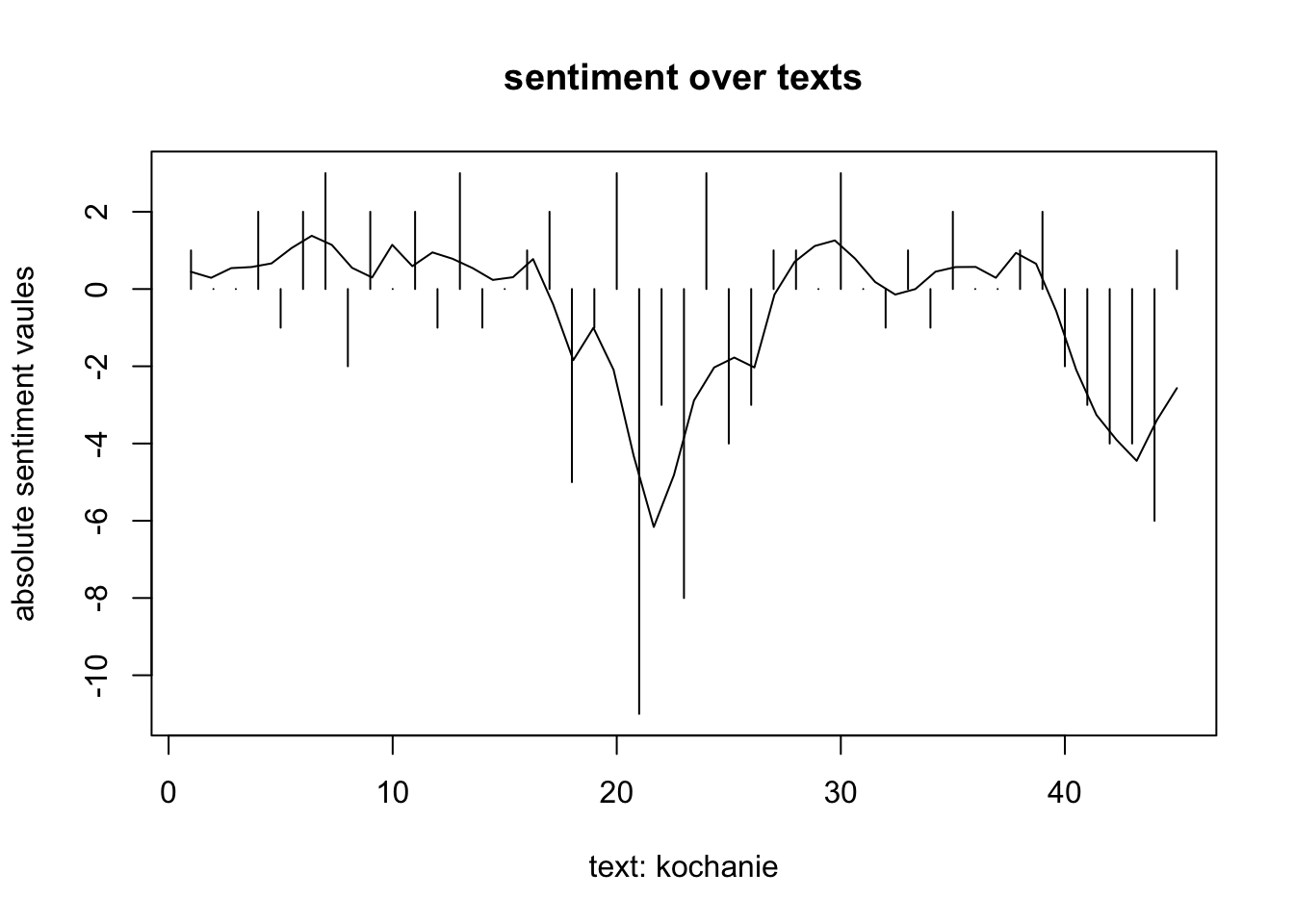
Für jeden einzelnen Text kann ein Wert bestimmt werden, der Aussagen darüber zuliesze, wo im Spektrum positive/negative sentiment sich dieser verorten läszt.
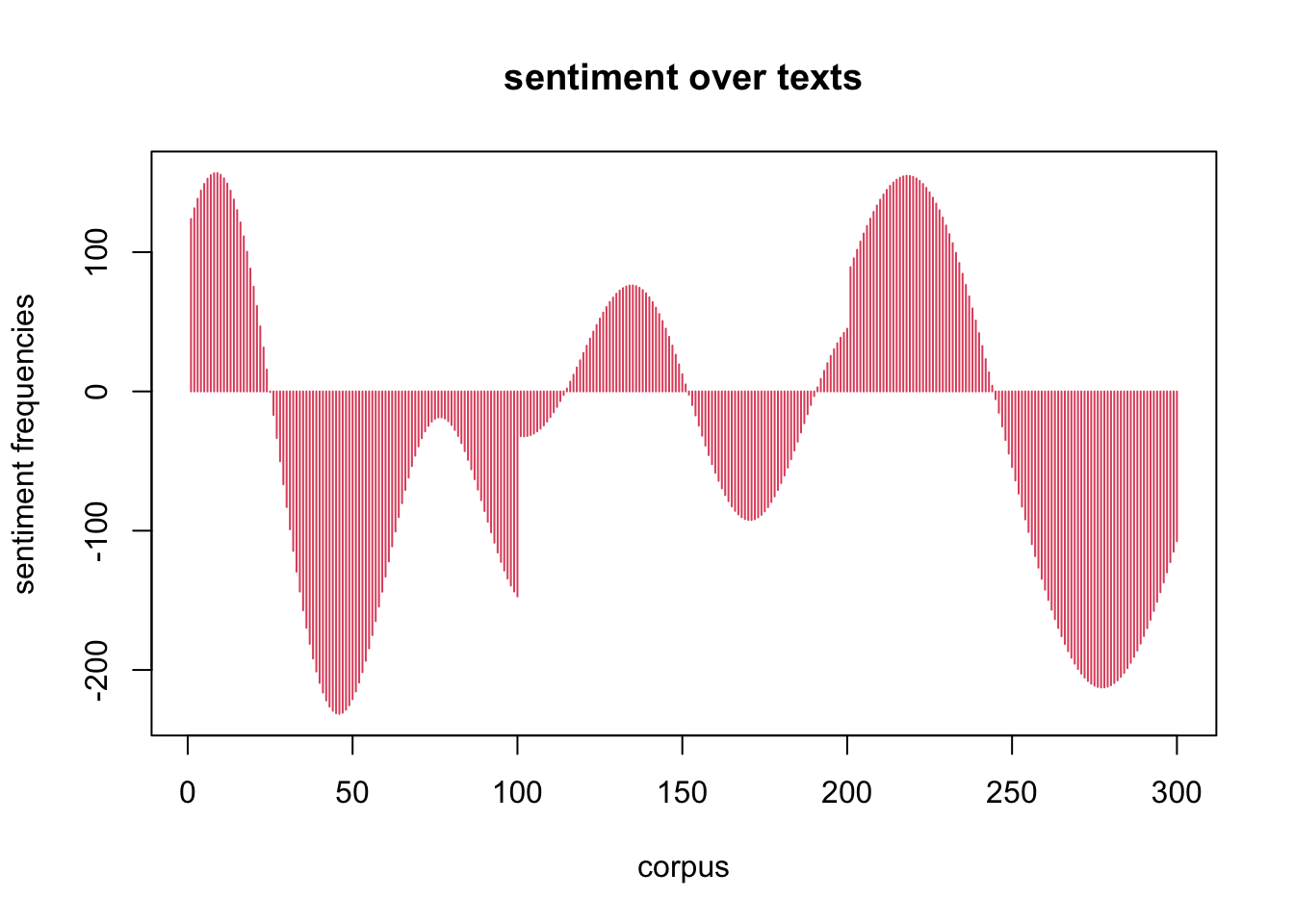
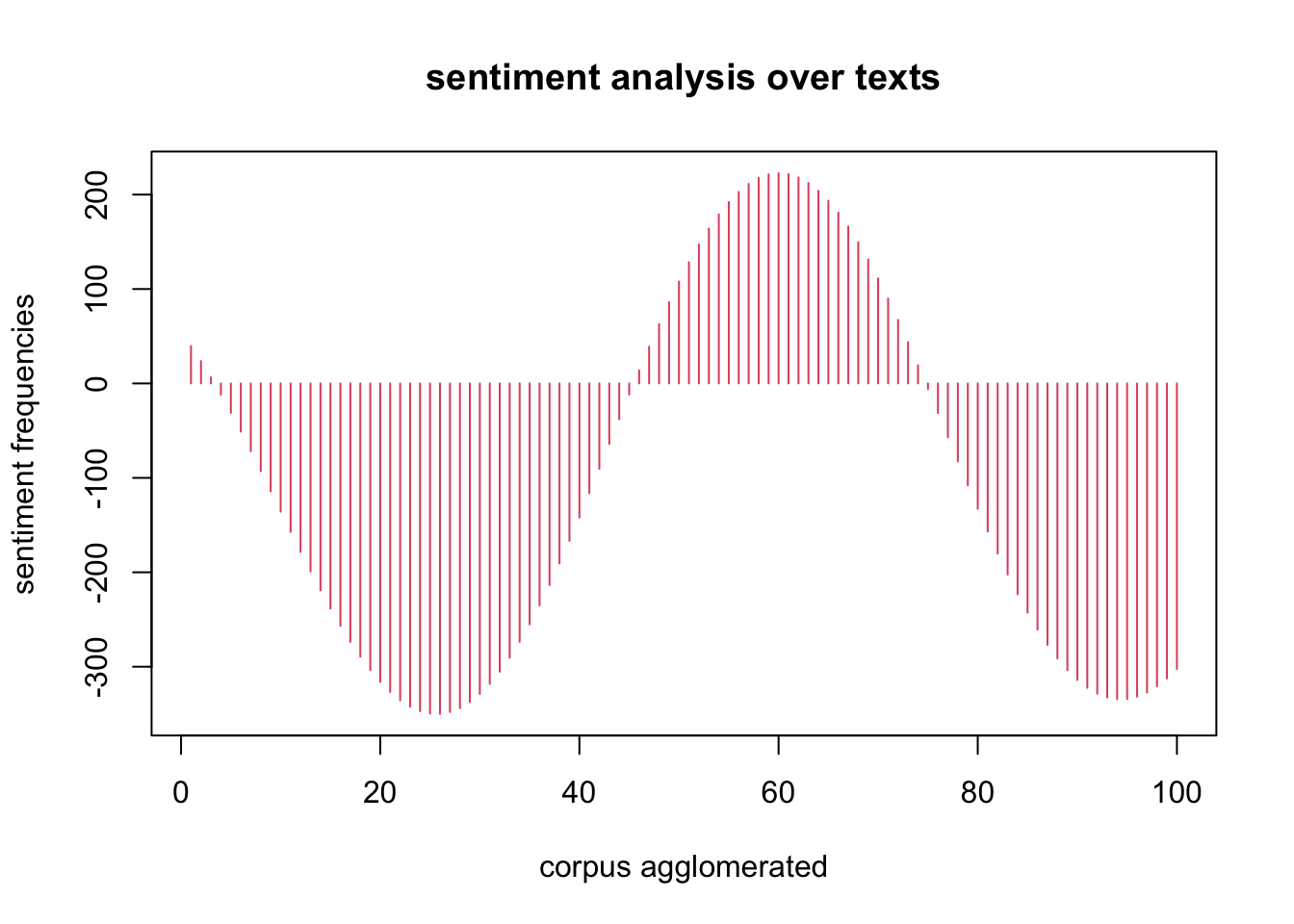
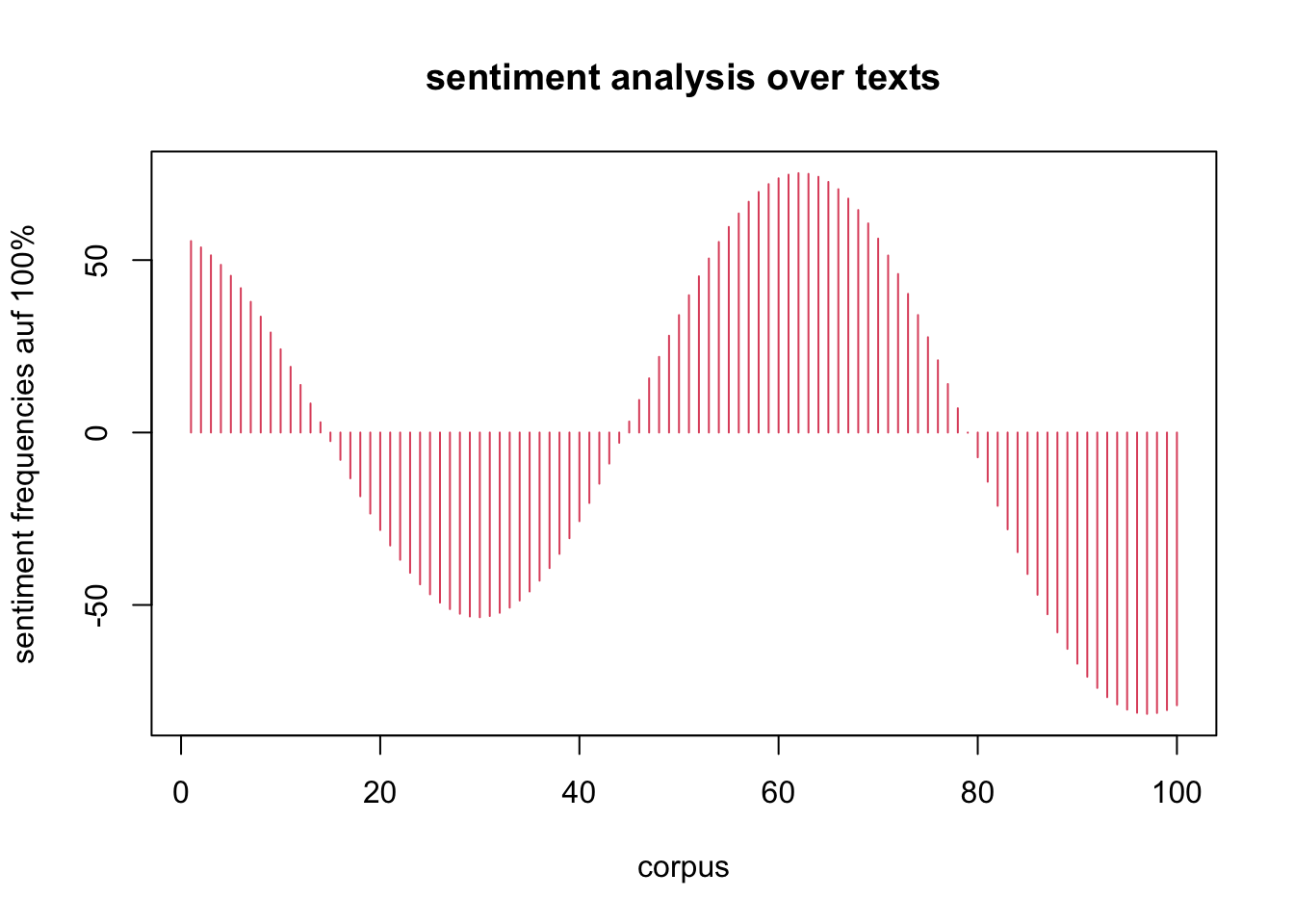
Die absoluten sentiment values werden weiterhin durch Fourier-Transformation auf die Gesamtheit des Korpus projiziert, um eine glatte, von der absoluten Position unabhängige Darstellung zu ermöglichen. (cf. Figure 10).
Welche Aussagen sich aus diesen Erkenntnissen ableiten lassen sollen, ist mir noch nicht ganz klar. I will elaborate on that.
in words
summary:
## $min
## $min$head
## [1] "kreisau, nebelvoliere"
##
## $min$book
## [1] "kochanie"
##
## $min$chapter
## [1] "krzyżowa, gefährten"
##
## $min$id
## [1] "142"
##
## $min$words
## du mich ich brust vogel halb
## 4 3 3 2 2 2
##
##
## $max
## $max$head
## [1] "an die kreisauer hunde" "nachtrag an die kreisauer hunde"
##
## $max$book
## [1] "kochanie" "kochanie"
##
## $max$chapter
## [1] "krzyżowa, gefährten" "krzyżowa, gefährten"
##
## $max$id
## [1] "143" "144"
##
## $max$words
## euch ihr gehört echo nur nicht
## 7 4 3 2 2 2
Zum Beispiel: Die höchsten sentiment Werte, hier in [chapter:] krzyżowa, gefährten, krzyżowa, gefährten, lassen sich in [text:] an die kreisauer hunde, nachtrag an die kreisauer hunde finden. Die most frequent words dieses Abschnitts sind euch, ihr, gehört, echo, nur, nicht, die niedrigsten finden sich im Text kreisau, nebelvoliere mit du, mich, ich, brust, vogel, halb.
visualisation
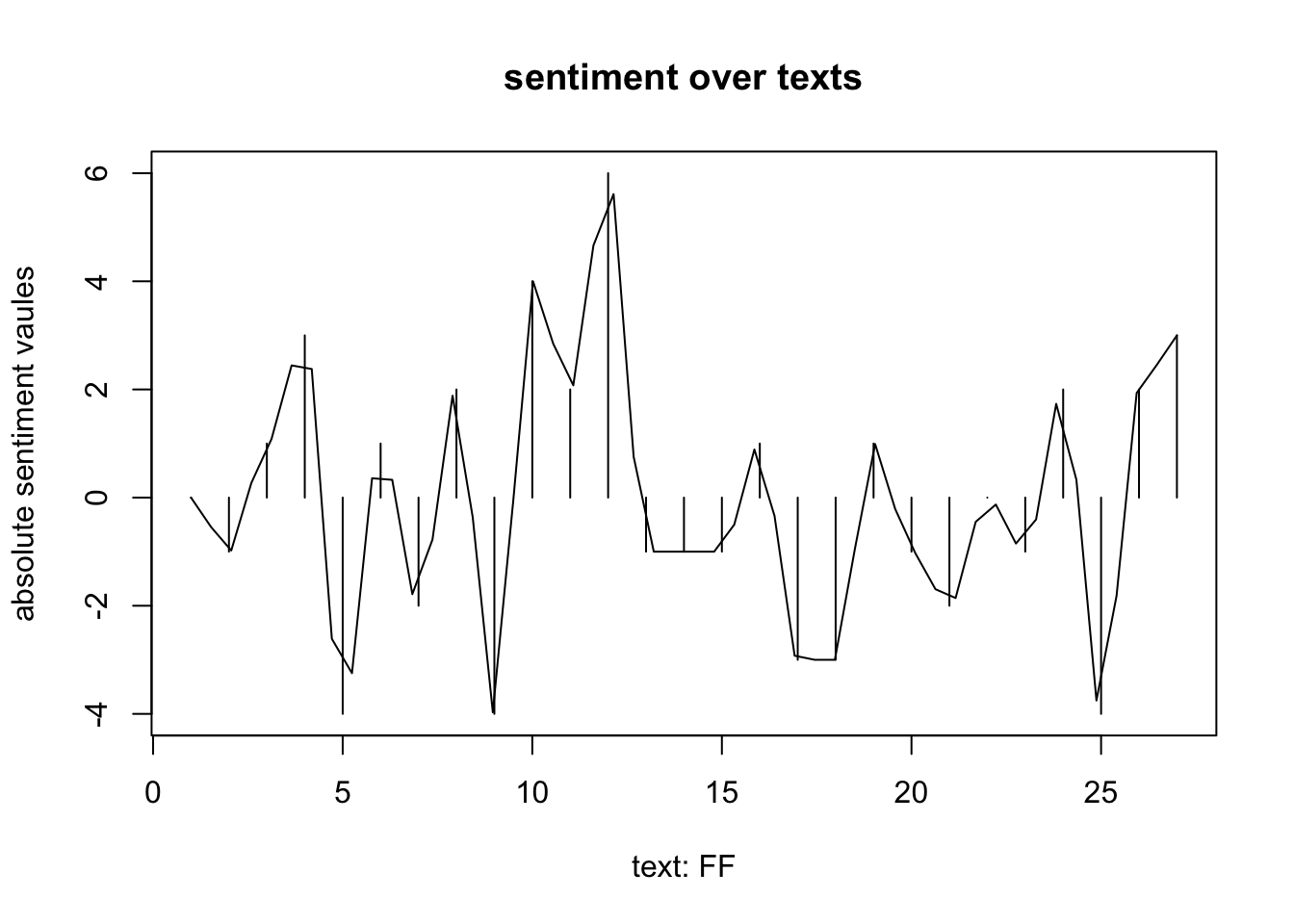
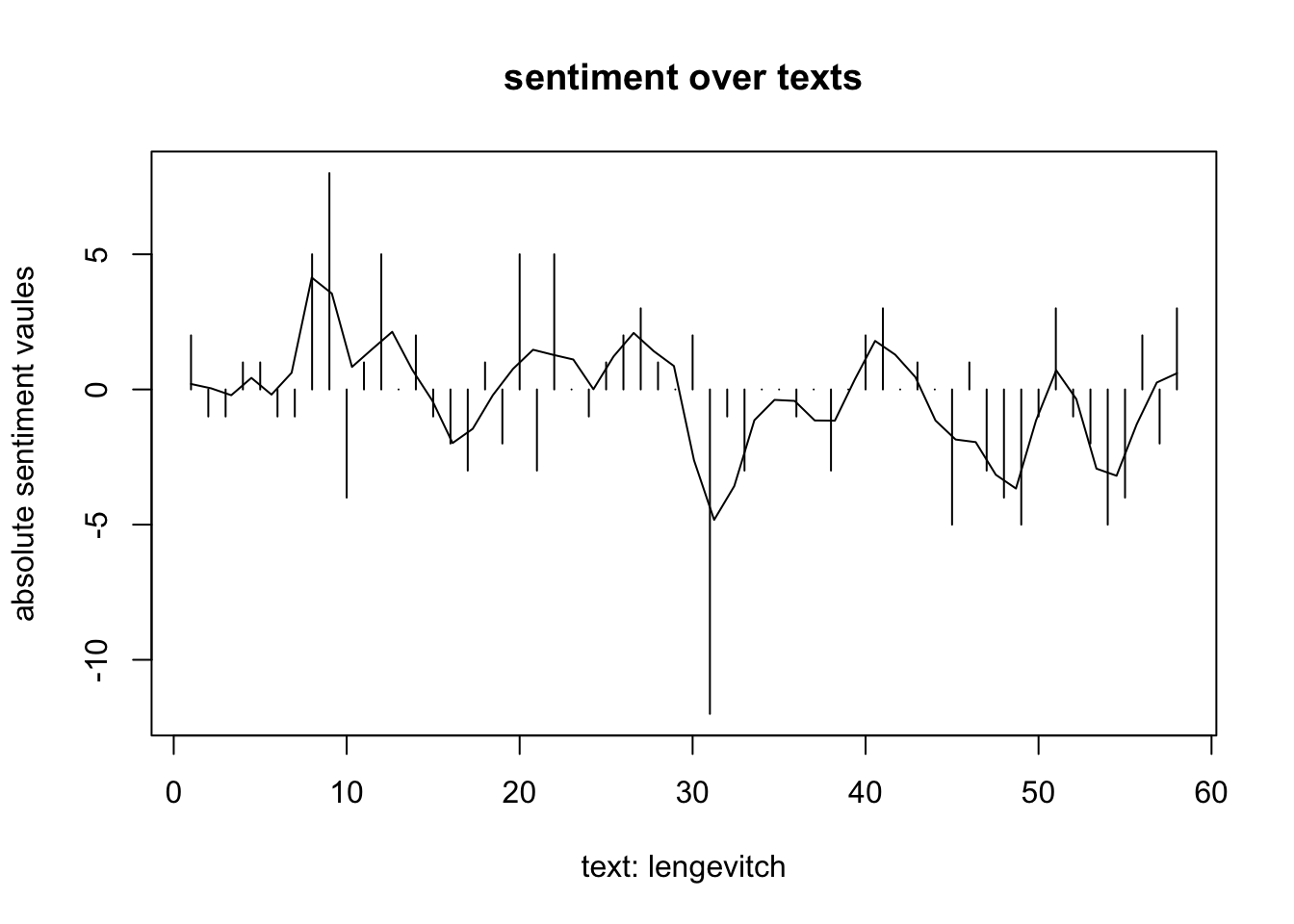
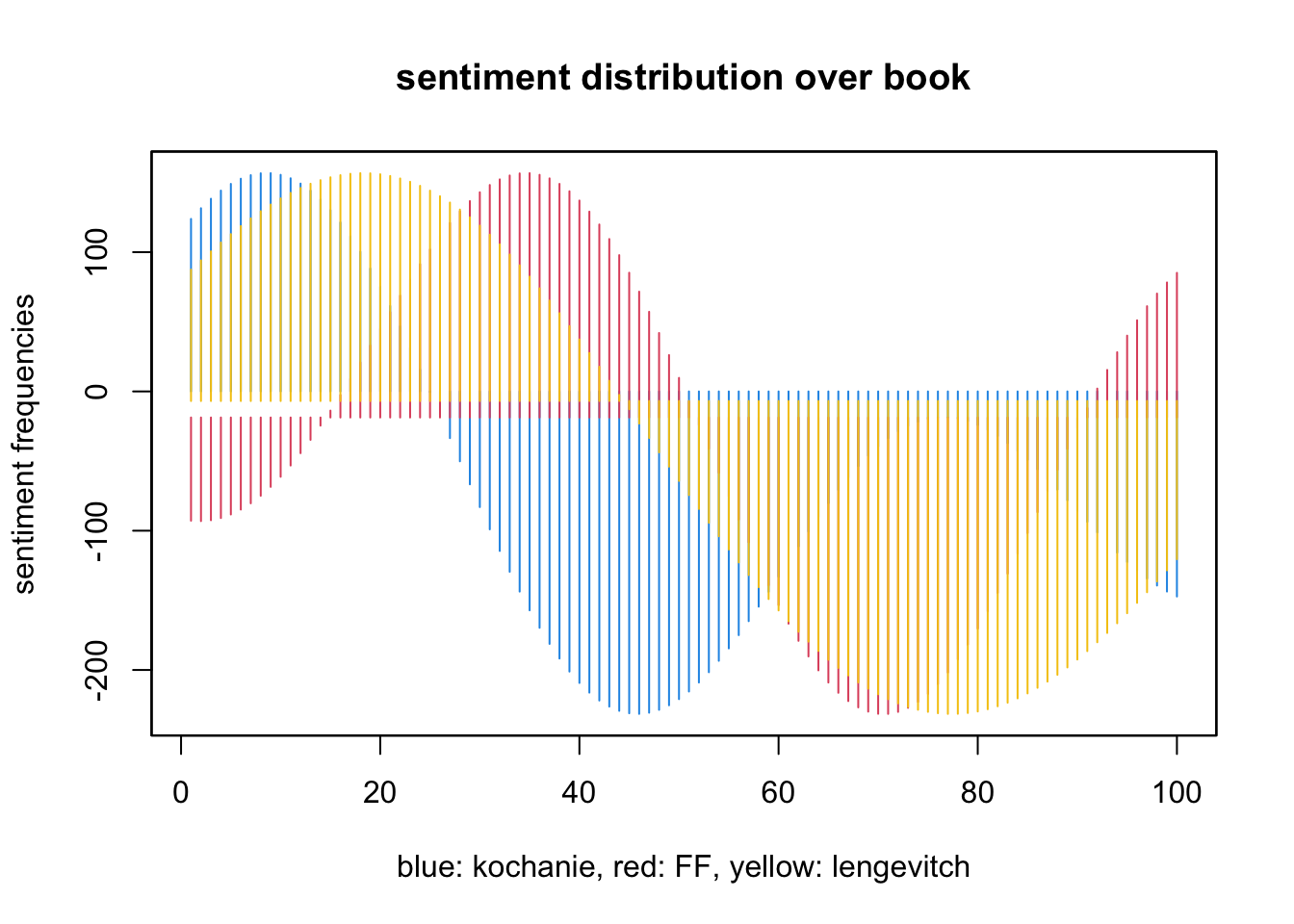
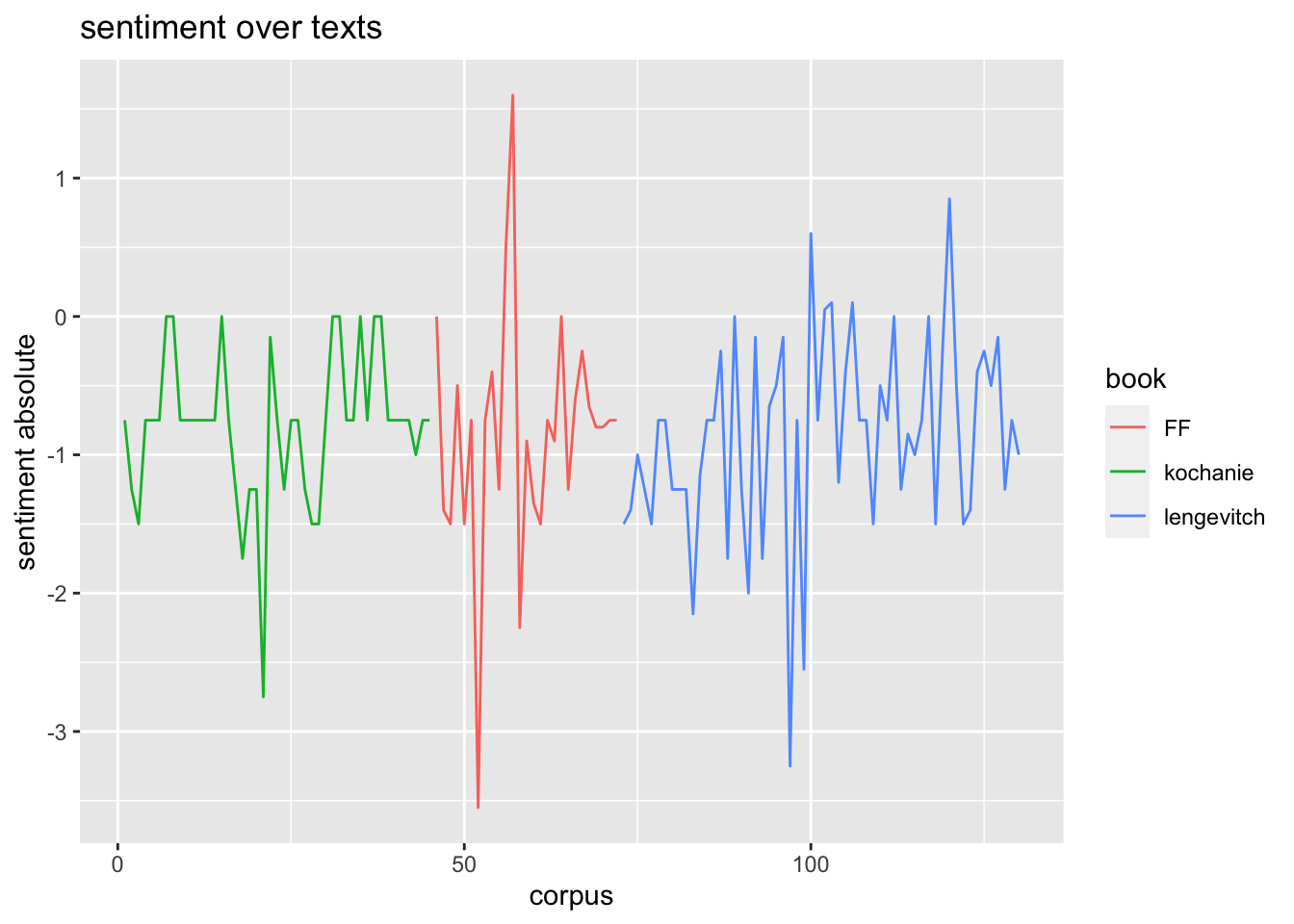
Wir sehen in den frequenzanalysierten Graphiken, dasz sich die relative Verteilung der sentiment values über die Bücher in der Tendenz unterscheidet. Während in kochanie und lengevitch schon zu Beginn Höhen verzeichnet sind, die Werte dann zur Buchmitte hin sinken, zeigt sich bei FF ein erster Wechsel von negativ zu positiv schon im ersten Drittel. Die Stimmung aller drei Bücher ist in der Mitte gleich negativ (bewertet), in kochanie aber schon wieder aufsteigend, falsche freunde weist die gröszten Schwankungen auf.
In kochanie weisen die Werte die niedrigste, in falsche freunde die höchste Varianz auf.
dependencies
Mit der Regressionsanalyse des R lme4 package (Bates et al. 2015) lassen sich hier Abhängigkeiten (Korrelationen) der sentiment values von verschiedenen Faktoren (chapter, book, multilingual elements) aufzeigen.
book/chapter dependency
summary:
## Linear mixed model fit by REML ['lmerMod']
## Formula: dta$sentiment ~ dta$book + (dta$book | dta$chapter)
## Data: dta
##
## REML criterion at convergence: 650.1
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.9330 -0.5158 0.0577 0.6694 2.7037
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## dta$chapter (Intercept) 0.2986 0.5465
## dta$bookFF 8.2772 2.8770 0.35
## dta$bookkochanie 0.2987 0.5465 -1.00 -0.35
## dta$booklengevitch 0.4123 0.6421 -0.87 -0.33 0.87
## Residual 8.9266 2.9877
## Number of obs: 131, groups: dta$chapter, 12
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) 9.795e-16 3.037e+00 0.000
## dta$bookFF -1.004e-15 4.386e+00 0.000
## dta$bookkochanie -5.556e-01 3.070e+00 -0.181
## dta$booklengevitch -1.991e-01 3.065e+00 -0.065
##
## Correlation of Fixed Effects:
## (Intr) dt$bFF dt$bkk
## dta$bookFF -0.693
## dta$bokkchn -0.989 0.685
## dt$bklngvtc -0.991 0.686 0.980
## optimizer (nloptwrap) convergence code: 0 (OK)
## boundary (singular) fit: see help('isSingular')
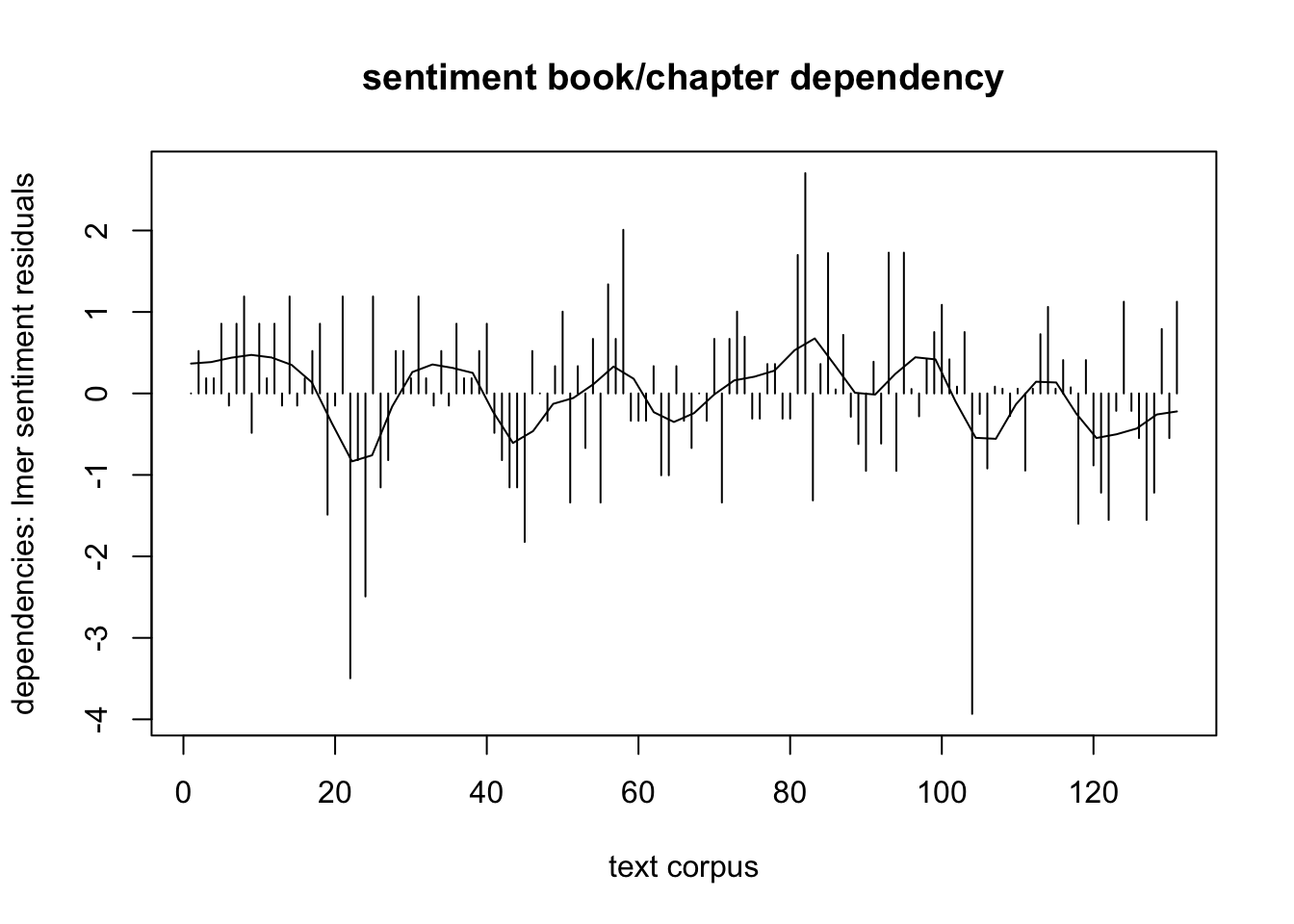
Es ist zu zeigen, dasz die Abhängigkeit durchaus variiert. Die relativen Korrelationswerte schwanken zwischen -82 und 75 (bei f(x)=x/100), zwischen 40-80% läszt sich gröszere Abhängigkeit beobachten, dh. hier sind die sentiment values am stärksten vom Kapitel beeinfluszt, beispielhaft beim Text[82:] , am wenigsten beim Text[104:] . (In der Regressionsanalyse wurden Veränderungen der Werte (Variablen) sentiment der Texte auf einen Zusammenhang mit Buch und Kapitel der jeweiligen Messung geprüft, dh. bestimmt, ob Buch und/oder Kapitel einen Einflusz auf den Wert haben.)
multiLX dependency
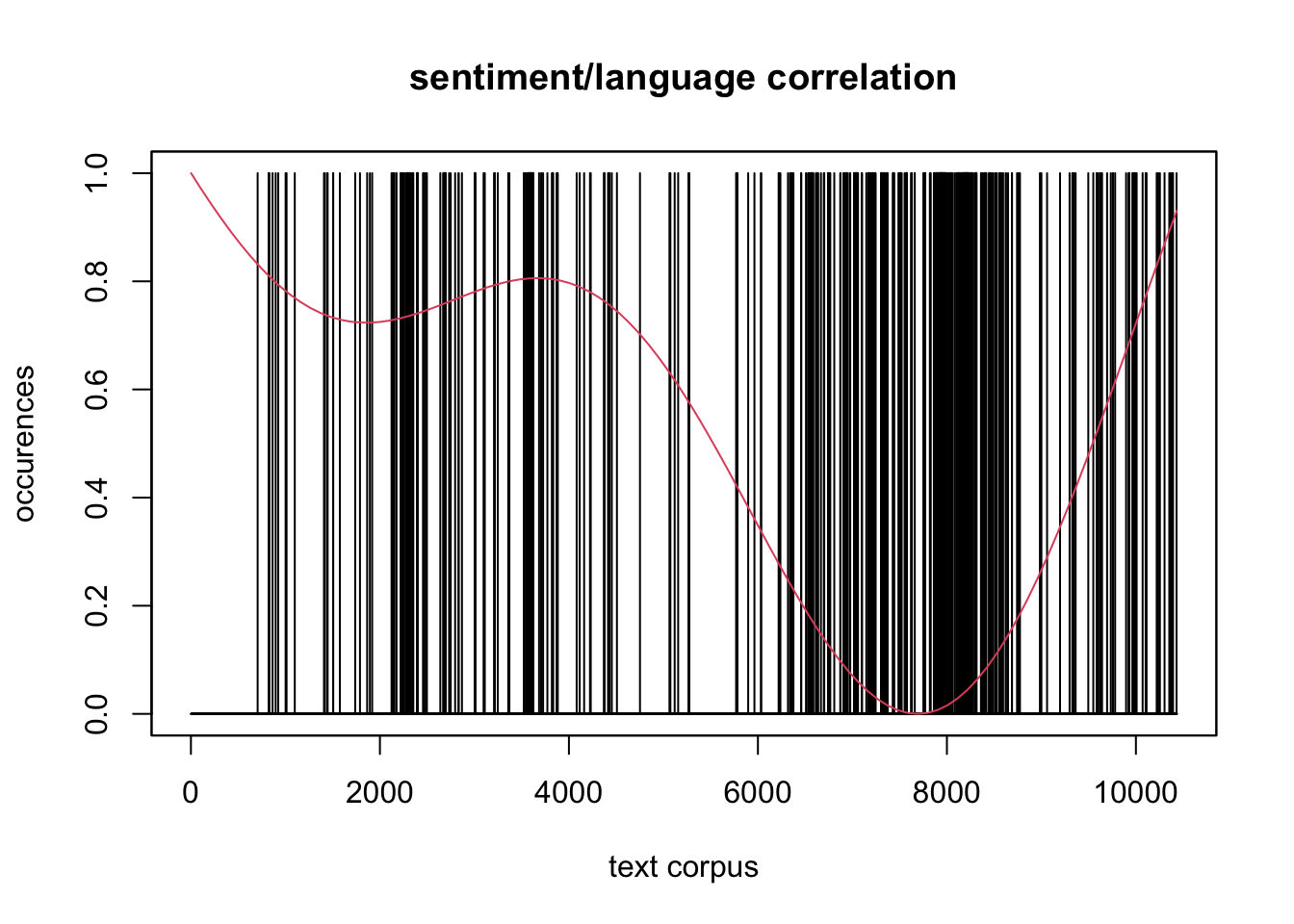
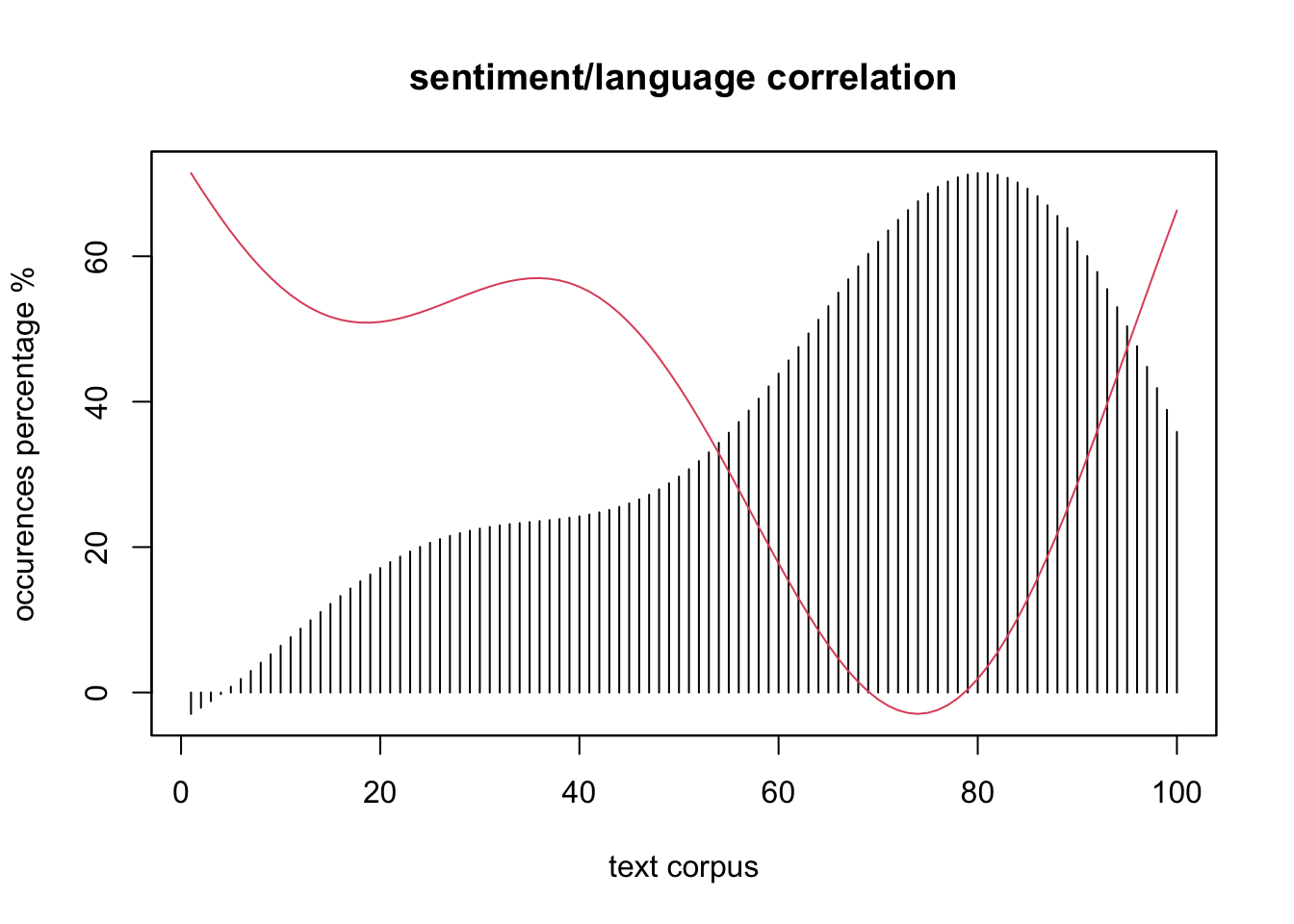
Weiterhin können wir versuchen, eine Abhängigkeit der sentiment values von der Verwendung multilingualer Elemente aufzuzeigen. Die verdichteten schwarzen Balken (cf. Figure 1) korrelieren hier mit der roten Linie der Stimmungswerte, was eine Abhängigkeit vermuten läszt.
summary:
## Linear mixed model fit by REML ['lmerMod']
## Formula: dta_t$sentiment ~ dta_t$book + (dta_t$book | dta_t$chapter) +
## (dta_t$lxp | dta_t$chapter) + (1 + dta_t$lxp) + (1 + dta_t$ttr)
## Data: dta_t
##
## REML criterion at convergence: 287.7
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -3.9484 -0.5075 0.0293 0.5177 3.4563
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## dta_t.chapter (Intercept) 0.2844653 0.53335
## dta_t$bookFF 0.2518810 0.50188 -0.03
## dta_t$bookkochanie 0.2843860 0.53328 -1.00 0.03
## dta_t$booklengevitch 0.2843925 0.53328 -1.00 0.03 1.00
## dta_t.chapter.1 (Intercept) 0.0394181 0.19854
## dta_t$lxp 0.0001687 0.01299 -1.00
## Residual 0.4794959 0.69246
## Number of obs: 131, groups: dta_t$chapter, 12
##
## Fixed effects:
## Estimate Std. Error t value
## (Intercept) -1.391441 1.194420 -1.165
## dta_t$bookFF -0.773382 1.166167 -0.663
## dta_t$bookkochanie -0.590773 0.918345 -0.643
## dta_t$booklengevitch -0.641043 0.917044 -0.699
## dta_t$lxp 0.005018 0.008272 0.607
## dta_t$ttr 1.391441 0.789468 1.763
##
## Correlation of Fixed Effects:
## (Intr) dt_$FF dt_t$bkk dt_t$bkl dt_t$l
## dta_t$bokFF -0.624
## dt_t$bkkchn -0.820 0.761
## dt_t$bklngv -0.839 0.769 0.976
## dta_t$lxp -0.083 -0.075 0.006 -0.057
## dta_t$ttr -0.661 0.072 0.133 0.160 0.125
## optimizer (nloptwrap) convergence code: 0 (OK)
## boundary (singular) fit: see help('isSingular')
Die Abhängigkeit der sentiment values vom Vorhandensein multilingualer Elemente läszt sich kurz umreiszen: Wir stellen den gröszten Zusammenhang mit [coefficient] 4.6e-05 bei dta_t$bookkochanie fest, die Differenz zu dta_t$bookFF beträgt 7.74, zu dta_t$booklengevitch 4.75 Punkte, der Abstand der Abhängigkeit hier also 2.99 Punkte.
Die Abhängigkeit der sentiment values von der type/token ratio der Texte ebenfalls kurz umrissen: Wir stellen den gröszten Zusammenhang mit [coefficient] 0.115873 bei dta_t$booklengevitch fest, die Differenz zu dta_t$bookFF beträgt 499.78, zu dta_t$bookkochanie 195.96 Punkte, der Abstand der Abhängigkeit hier also 303.82 Punkte.
corpus play
Das Folgende zeigt einen Text, dem ein Algoritmus zugrundeliegt, der roughly die Wahrscheinlichkeit des Vorhandenseins eines Wortes an der jeweiligen Position im Text, über den gesamten Korpus betrachtet, bestimmt. Es tritt also jedes Wort dieses künstlichen Textes am wahrscheinlichsten an dieser Stelle auf, szsg. ein sehr simples transformer experiment, ohne jegliche Berücksichtigung semantisch-syntaktischer Kategorien und (noch) weit von einem lernfähigen Algorithmus entfernt
most probable text
13506.ST: Uljana Wolf / GPTestee
<<<
ein a a a einfachen a a i der und ich i in b in ein i a a er a es in in a u h in i a der in ein a der an in a i er er in es a a und in in in u er ich i in a in an in die i in er in u a in a a den in in a a i in ich ein oder in i in in to in in a u wo das und in an ein der a es in der er der mit im ein die der es nicht die die b u t wir in die an ihre in ein ewig ich oder oder ich in nicht gehört ihr muttersprache lernen platzt er herkunft is ich decke richtung u ich sich nicht dinge puckerten darin too small vom mesmer getroffen ungelenkten wagten war der anders anders anders er anders anders anders anders anders am es ein rage dann tee aber wenn es zeit ist für orangen ist es keine zeit no time at all für durst für wasser ich sich arrangieren lassen weil orangen sind ihr eignes rangiermaterial weil züge brücken ich schiffchen keeps me going unbeschwichtigt go nicht go lack use to her weil orangen kommunizieren durch die zeiten orangen oder rundum residenzpflicht orangen oder in eine grenzsicht its like were in prison es trees and animals were at the für of the world wenn es die ist für tarnopol ist es keine zeit not time at all für weltenden schlossvorhänge papiervorgänge weil orangen sind lebensmittelpunkt weil ein mangel mangel geh sei ihr von nutzen geh die esse putzen dass der doktor wiederkommt dass nicht bis die türen aufgehen und man seine sippe auf die straße setzt sie sagen a family is what one blumenschmuggler ihre dunklen wege durch europa ziehen sie sagen we make a business with such bodies with blüten poesie und ich sage we will see what can all the green stuff be recht auf seinen freigang hat aber dass orangen
<<< fin.
B. REF:
Bates, Douglas, Martin Mächler, Ben Bolker, and Steve Walker. 2015.
“Fitting Linear Mixed-Effects Models Using Lme4.” Journal of Statistical Software 67 (1): 1–48.
https://doi.org/10.18637/jss.v067.i01.
Jockers, Matthew L. 2015.
“Revealing Sentiment and Plot Arcs with the Syuzhet Package Matthew L. Jockers.” https://www.matthewjockers.net/2015/02/02/syuzhet/.
Wolf, Uljana. 2005. Kochanie Ich Habe Brot Gekauft: Gedichte / Uljana Wolf. 1. Aufl. Reihe Lyrik 5. Idstein: Kookbooks.
———. 2009. Falsche Freunde: Gedichte / Uljana Wolf. 1. Aufl. Kookbooks : Reihe Lyrik 15. Idstein: kookbooks.
———. 2013. Meine Schönste Lengevitch: Gedichte / Uljana Wolf. 1. Auflage. Reihe Lyrik Band 32. Berlin: kookbooks.
———. 2021. Etymologischer Gossip: Essays Und Reden / Uljana Wolf. 1. Auflage. Kookbooks Reihe Essay 7. Berlin: kookbooks.
LS0tCiMtLS0gb2ZmaWNpYWwgLS0tIwojIEhhdXNhcmJlaXQgaW0gU2VtaW5hcjogRHluYW1pa2VuIHBvc3RkZXV0c2NoZXIgR2VnZW53YXJ0c2xpdGVyYXR1ciwgQ2xhcmEgTGlzbywgU1MyMDIyIEZVQgojIGltIEZhY2g6IEFsbGdlbWVpbmUgdW5kIFZlcmdsZWljaGVuZGUgTGl0ZXJhdHVyd2lzc2Vuc2NoYWZ0ZW4KIyBlaW5nZXJlaWNodCB2b24gU3RlcGhhbiBTY2h3YXJ6CiMgQWJnYWJlOiBkdWUKCnRpdGxlOiAiRFlOIEhBIC8gU1MyMiBGVUIgLyBMaXNvIgphdXRob3I6ICJzdC4gc2Nod2FyeiIKZGF0ZTogImByIFN5cy50aW1lKClgIgp6b3Rlcm86IEFWTF9keW4Kb3V0cHV0OgogIGJvb2tkb3duOjpwZGZfZG9jdW1lbnQyOgogICAgZXh0cmFfZGVwZW5kZW5jaWVzOiBbImZsb2F0Il0KICBib29rZG93bjo6aHRtbF9kb2N1bWVudDI6CiAgICBnbG9iYWxfbnVtYmVyaW5nOiBUUlVFCiAgICBudW1iZXJfc2VjdGlvbnM6IFRSVUUKICAgIGNvZGVfZG93bmxvYWQ6IHllcwogICAgdG9jOiB5ZXMKICAgIHRvY19kZXB0aDogNAogICAgdG9jX2Zsb2F0OgogICAgICBjb2xsYXBzZWQ6IG5vCiAgICAgIHNtb290aF9zY3JvbGw6IG5vCiAgICAgICN0b2MtZGVwdGg6IDQKICAgIHNlbGZfY29udGFpbmVkOiBGQUxTRSAjVFJVRSBmb3Igc3RhbmRhbG9uZSBodG1sIHBhZ2Uga25pdAojY3NzOiAuLi9zdHlsZV9IQS5jc3MKI3N3YXAgLyBkZWNvbW1lbnQgZmYgLmJpYi8uY3NzIHJlZmVyZW5jZXMgZm9yIHNlbGYgY29tcGlsZSAuUm1kIHRvIGh0bWwKI2JpYmxpb2dyYXBoeTogaHR0cHM6Ly9yYXcuZ2l0aHVidXNlcmNvbnRlbnQuY29tL2VzdGVlc2Nod2Fyei9ESF9lc3NhaXMvbWFpbi9zZWN0aW9ucy9EWU4vRFlOX0hBL0RZTl9IQS5iaWIKICAgIGNzczogaHR0cHM6Ly9zY2hvb2wuZGgtaW5kZXgub3JnL3B1YmxpYy9wYXBlcnMvMDExL3N0eWxlX0hBLmNzcwojIG91dHB1dDoKIyAgIHBkZl9kb2N1bWVudDoKIyAgICAgbWFpbmZvbnQ6IEFyaWFsCiMgICAgIGxhdGV4X2VuZ2luZTogcGRmbGF0ZXgKIyAgICAgZ2xvYmFsX251bWJlcmluZzogVFJVRQojICAgICBudW1iZXJfc2VjdGlvbnM6IFRSVUUKIyAgICAgZXh0cmFfZGVwZW5kZW5jaWVzOiBbImZsb2F0Il0KIyBvdXRwdXQ6CiMgICBwZGZfZG9jdW1lbnQ6CiMgICAKIyBkb2N1bWVudGNsYXNzOiBhcnRpY2xlCiMgcGFwZXJzaXplOiBhNAojIGxpbmVzdHJldGNoOiAxLjUKIyBsaW5rcy1hcy1ub3RlczogZmFsc2UKIyBmb250ZmFtaWx5OiBpd29uYQojIGZvbnRzaXplOiAxNnB0CiMgLS1udW1iZXItc2VjdGlvbnM6IHRydWUKIyAKIyBkb2N1bWVudGNsYXNzOiBib29rICAgIAojICAgICBwYXBlcnNpemU6IGE0CiMgICAgIGxpbmVzdHJldGNoOiAxLjUKIyAgICAgZm9udHNpemU6IDE2cHQKIyAgICAgZm9udGZhbWlseTogQXJpYWwKIyAgICAgbGlua2NvbG9yOiBibHVlCiMgICAgIGxpbmtzLWFzLW5vdGVzOiBmYWxzZQpudW1iZXJfc2VjdGlvbnM6IHllcwpnbG9iYWxfbnVtYmVyaW5nOiB5ZXMKbGlua2NvbG9yOiBibHVlICAjI2xlZnRsZWZ0CnRvYy1kZXB0aDogNCAgIyNsZWZ0bGVmdAoKCmJpYmxpb2dyYXBoeTogRFlOX0hBLmJpYgotLS0KIyBBLiBoZWFkCkhhdXNhcmJlaXQgaW0gRmFjaCBBVkwsIE1vZHVsICJWZXJnbGVpY2hlbmRlIExpdGVyYXR1cmdlc2NoaWNodGUiLiAgIApTZW1pbmFyOiAiRElFIFNDSMOWTlNURU4gTEVOR0VWSVRDSEVTOiBEWU5BTUlLRU4gREVSIFBPU1QtREVVVFNDSEVOIEdFR0VOV0FSVFNMWVJJSyIuICAgIApEb3plbnRpbjogQ2hpYXJhIExpc28uICAgClNvU2UgMjAyMi4gICAKZWluZ2VyZWljaHQ6IGByIGRhdGVfYWJnYWJlYCAgIAplZGl0ZWQ6IGByIGRhdGVfZWRpdGAgICAKYW5kZXJlcyBmb3JtYXQ6IGByIG1lc3NhZ2VgICAgCgpgYGB7ciBzZXR1cCwgaW5jbHVkZT1GQUxTRX0Ka25pdHI6Om9wdHNfY2h1bmskc2V0KGVjaG8gPSBGQUxTRSkKa25pdHI6Om9wdHNfY2h1bmskc2V0KGZpZy5wb3MgPSAiSCIsIG91dC5leHRyYSA9ICIiKQoja25pdHI6Om9wdHNfa25pdCRnZXQoIm91dC5mb3JtYXQiPSJodG1sIikKI21pbmkgY3JpdGljYWw6IGRvbnQgZmluZCByZWxhdGl2ZSBmaWxlcyBpbiBwYXRoCiNrbml0cjo6b3B0c19rbml0JHNldChyb290LmRpcj0iLyIpCiNrbml0cjo6b3B0c19rbml0JHNldChiYXNlLmRpciA9ICJsb2NhbC9EWU4va25pdGVzc2FpIikgI2NyZWF0ZXMgdGhpcyBkaXIgaW4gUm1kIGRpcmVjdG9yeSwgaW5jbHVkaW5nIHh4eC5maWxlcywgaWYgb3V0IGNhbnQgY3JlYXRlIG91dHB1dCBkaXIKI2tuaXRyOjpvcHRzX2tuaXQkc2V0KGJhc2UuZGlyID0gIi8iKSAjY3JlYXRlcyB0aGlzIGRpciBpbiBSbWQgZGlyZWN0b3J5LCBpbmNsdWRpbmcgeHh4LmZpbGVzLCBpZiBvdXQgY2FudCBjcmVhdGUgb3V0cHV0IGRpcgoja25pdHI6Om9wdHNfa25pdCRzZXQoYmFzZS5kaXIgPSAifi9ib3hIS1cvMjFTL0RIL2dpdGgvREhfZXNzYWlzL3NlY3Rpb25zL0RZTi9EWU5fSEEiKQojZ2V0d2QoKQojRVdBLCBsYXBzaQoja25pdHI6Om9wdHNfa25pdCRzZXQocm9vdC5kaXI9In4vYm94SEtXL1VOSS8yMVMvREgiKQoja25pdHI6Om9wdHNfa25pdCRzZXQoYmFzZS5kaXIgPSAifi9ib3hIS1cvVU5JLzIxUy9ESC9naXRoL0RIX2Vzc2Fpcy9zZWN0aW9ucy9EWU4vRFlOX0hBIikKCmBgYAoKYGBge3IgYmliLCBldmFsPVRSVUUsIGVjaG89RkFMU0UsIHdhcm5pbmc9RkFMU0UsbWVzc2FnZT1GQUxTRX0KbGlicmFyeShodHRyKQojZmV0Y2ggem90ZXJvIC5iaWIgb25saW5lCiNzaGFyZSA8LSBydW5pZigxKQpyZXNwb25zZTwtR0VUKCJodHRwczovL2FwaS56b3Rlcm8ub3JnL2dyb3Vwcy80NzEzMjQ2L2NvbGxlY3Rpb25zLzlMTlJSSlFOL2l0ZW1zL3RvcD9mb3JtYXQ9YmlidGV4IikKYmliPC1odHRyOjpjb250ZW50KHJlc3BvbnNlLCJ0ZXh0IikKeTwtdGVtcGZpbGUoInJlZiIsZmlsZWV4dCA9ICIuYmliIikKd3JpdGVMaW5lcyhiaWIseSkKdDwtU3lzLnRpbWUoKQojdGY8LWZvcm1hdCh0LCIlYSAlYiAlZCAlWSAoJUguJU0pIikKdGY8LWZvcm1hdCh0LCIlWSVtJWQoJUguJU0pIikKI3RmCiMgdGNzdjwtcGFzdGUoMSx0LCJybWRfc3RhcnQiLHNlcCA9ICIsIikKIyBkdDwtZmlsZSgiZGF0ZXN0YW1wX2N1cnJlbnQzLmNzdiIsb3BlbiA9ICJhIikKIyB3cml0ZUxpbmVzKHRjc3YsZHQpCiMgY2xvc2UoZHQpCmBgYAotLS0KYmlibGlvZ3JhcGh5OiAiYHIgeWAiCmRhdGU6IGByIHRpbWVzdGFtcF9hY3RgCi0tLQpgYGB7ciBzb3VyY2VzLCBldmFsPUZBTFNFLCBlY2hvPUZBTFNFLCBjb2xsYXBzZT1UUlVFLCB3YXJuaW5nPUZBTFNFLG1lc3NhZ2U9RkFMU0V9CiNsaWJyYXJ5KG1vbmdvbGl0ZSkKI2xpYnJhcnkoanNvbmxpdGUpCmxpYnJhcnkoc3l1emhldCkKbGlicmFyeShyZWFkcikKbGlicmFyeShnZ3Bsb3QyKQpsaWJyYXJ5KGxtZTQpCmxpYnJhcnkoc3RyaW5naSkKbGlicmFyeShzdHJpbmdyKQpsaWJyYXJ5KHJtYXJrZG93bikKbGlicmFyeShxdWFudGVkYSkKCgoKI3Jvb3Q8LSIvVXNlcnMvbGlvbi9ib3hIS1cvMjFTL0RILyIKI2xvY2FsPC1wYXN0ZTAocm9vdCwibG9jYWwvRFlOLyIpCiNzZXR3ZCgifi9ib3hIS1cvMjFTL0RIIikKI3NyYzwtIndvbGZfRkZfMS5qc29uIgojc3JjPC1wYXN0ZTAobG9jYWwsIndvbGZfRkYtTEVOXzEuanNvbiIpCiNnZXR3ZCgpCiNzcmM8LSIuLi8uLi8uLi8uLi8uLi9sb2NhbC9SL2NyZWRfZ2VuZXIuY3N2IgojICBjcmVkPC1yZWFkLmNzdihzcmMpCiMgIGNvbjwtIG1vbmdvKGNvbGxlY3Rpb24gPSAid29sZmRiMDAzIiwgZGIgPSJkZWFkZW5kIiwgdXJsPWNyZWQkdXJsW2NyZWQkcT09Im1vbmdvZGIiXSkKICMgICBkdGE8LWNvbiRmaW5kKCd7fScpCiNsb2NhbCBkYXRhOgogICAgIyBzcmM8LSAgICIuLi9kYi93b2xmZGIwMDMuY3N2IgogICAgIyBzcmNfbHg8LSIuLi9kYi90b2tlbnNNdWx0aUxYX20uY3N2IgogICAgIyBzcmNfc3Q8LSJodHRwczovL3Jhdy5naXRodWJ1c2VyY29udGVudC5jb20vZXN0ZWVzY2h3YXJ6L0RIX2Vzc2Fpcy9tYWluL3NlY3Rpb25zL0RZTi9EWU5fSEEvY29ycHVzL3dvbGZfTEVfc3RvcHdvcmRzLmNzdiIKCiAgICBkdGE8LXJlYWRfY3N2MihzcmNfZGIpCiAgICMgZHRhX3Q8LWdldF90eXBlcyhkdGEsMSkKICAgIGx4dGFibGU8LXJlYWRfY3N2MihzcmNfbHgpCiAgICBtbHg8LXN1YnNldChseHRhYmxlLGx4dGFibGUkbXVsdGk9PSJtdWx0aUxYIikKI2dldHdkKCkKICAgIGR0YV9zZjwtZHRhCiNrPC0yCiNkdGF0eHQ8LWFzLmRhdGEuZnJhbWUoZnJvbUpTT04oc3JjKSkKI2R0YXR4dDwtKGZyb21KU09OKHNyYykpCiNjYXQoImxvYWQgVEVJIGZyb206IixzcmMpCiAgICMjIyMjIyMjICNzcmNfc2U8LSJEWU5fSEFfc2VtYW50aWNzLlIiCiNzb3VyY2UoIi9naXRoL0RIX2Vzc2Fpcy9zZWN0aW9ucy9EWU4vRFlOX0hBL0RZTl9IQV9zZW1hbnRpY3MuUiIpCiAgIHNvdXJjZSh0ZW1wc2UpCiAgbGM8LWxlbmd0aChkdGEkY29udGVudCktMQogIG1md19kdGE8LWxpc3QoKQpmb3IgKGsgaW4gMjogbGVuZ3RoKGNoYXB0ZXJfZXgpKXsKICAKCm1md19kdGFbW2tdXTwtbWZ3KGR0YSxrKQp9CiAgI25ldWVyZGluZyBSIHdhdGVybWFyayB3aXRoIHBsb3QoY2FycykgYXMgZmlyc3QgaW1nIHNvdXJjZT8gCiAgI3RyeSBwcmV2ZW50CiAgICB0b3A8LTEwMDAwCiAgYTwtc2FtcGxlKHRvcCx0b3ApCiAgYzwtc3FydChsZW5ndGgoYSkpCiAgYjwtbWF0cml4KGEsYyxjKQppbWFnZShiLHhheHQ9Im4iLHlheHQ9Im4iKSAgCgpgYGAKCi0tLQoKIyBlaW5sZWl0dW5nCldpciB3ZXJkZW4gaW0gRm9sZ2VuZGVuIGRlbiBWZXJzdWNoIHVudGVybmVobWVuLCBhdXMgZWluaWdlbiBzdGF0aXN0aXNjaGVuIEJlcmVjaG51bmdlbiBBdXNzYWdlbiB6dW0gbHlyaXNjaGVuIFdlcmsgVWxqYW5hIFdvbGZzIGFienVsZWl0ZW4uIE9iIGRhcmF1cyBFcmtlbm50bmlzc2UgaGluc2ljaHRsaWNoIGRlcyBBc3Bla3RzICpwb3N0ZGV1dHNjaCogZXJ3YWNoc2VuLCBrw7ZubmVuIHdpciBub2NoIG5pY2h0IHNhZ2VuLgpEaWUgQXJiZWl0IHdpcmQgZXhwbG9yYXRpdiB2b3JnZWhlbiwgZGguIHVuc2VyIEVya2VubnRuaXNpbnRlcmVzc2UgaXN0IGR1cmNoYXVzIHVuZ2VyaWNodGV0LiBXaXIgd29sbGVuIHdlc2VudGxpY2ggZWluaWdlIE1ldGhvZGVuIHp1ciBBbndlbmR1bmcgYnJpbmdlbiwgZGllIGdlZWlnbmV0IGVyc2NoZWluZW4sIHdlaXRlcmUgbGl0ZXJhdHVyd2lzc2Vuc2NoYWZ0bGljaGUgRnJhZ2VzdGVsbHVuZ2VuIHp1IGJlYW50d29ydGVuLiBFaW5lIHdlaXRlciBnZWZhc3N0ZSBBdWZnYWJlbnN0ZWxsdW5nIGRpZXNlciBBcmJlaXQgd8O8cmRlIGNhLiBsYXV0ZW46CgojIyB0YXNrCkJlc3RpbW11bmcgY2hhcmFrdGVyaXN0aXNjaGVyIE1lcmttYWxlIGltIGx5cmlzY2hlbiBXZXJrIFVsamFuYSBXb2xmcyBtaXRoaWxmZSBzdGF0aXN0aXNjaGVyIE1ldGhvZGVuLiAKCiMgenVyIGF1dG9yaW4KVWxqYW5hIFdvbGYsIGRlciDDlmZmZW50bGljaGtlaXQgc2VpdCAyMDA1IGR1cmNoIGlocmUgR2VkaWNodGUgYmVrYW5udCwgd3VyZGUgMjAwNiBmw7xyIGlociBEZWLDvHQgKmtvY2hhbmllIGljaCBoYWJlIGJyb3QgZ2VrYXVmdCogKGtvb2tib29rcyAyMDA1KSBtaXQgZGVtIFBldGVyLUh1Y2hlbC1QcmVpcyBhdXNnZXplaWNobmV0IHVuZCB2ZXLDtmZmZW50bGljaHRlIHNlaXRkZW0gbmViZW4gw5xiZXJzZXR6dW5nZW4gdW5kIGVzc2F5aXN0aXNjaGVuIFNjaHJpZnRlbiB6d2VpIHdlaXRlcmUgR2VkaWNodGLDpG5kZSwgZWJlbmZhbGxzIGJlaSAqa29va2Jvb2tzKi4gRG9ydCBpc3Qgc2llIGluIGVpbiBlbmdlcyBOZXR6d2VyayBqdW5nZXIgZGV1dHNjaHNwcmFjaGlnZXIgQXV0b3I6aW5uZW4gZWluZ2VidW5kZW4sIGRpZSBzaWNoIGF1Y2ggKGhpZXIgenVtIEFzcGVrdCAqcG9zdGRldXRzY2gqKSBtZWhyaGVpdGxpY2ggZHVyY2ggaWhyZSBBZmZpbml0w6R0IHp1IG1laHItIG9kZXIgcG9seWxpbmd1YWxlciBEaWNodHVuZyBhdXN6ZWljaG5lbi4gRXMgZ2lidCBiZWkga29vayBrYXVtIERpY2h0ZXI6aW5uZW4sIGRlcmVuIFdlcmsgbmljaHQgaXJnZW5kd2llIE1laHJzcHJhY2hpZ2tlaXQga8O8bnN0bGVyaXNjaCBhdXNkcsO8Y2t0LCBkYW1pdCBhcmJlaXRldC4gTmljaHQgYWxsZSB2ZXJlaW50IGVpbmUgd2lya2xpY2ggKG11dHRlcnNwcmFjaGxpY2hlIFByb3ZlbmllbnopIGluIGFuZGVyZW4gZXVyb3DDpGlzY2hlbiB1LmEuIFNwcmFjaGVuIGFscyBkZW0gRGV1dHNjaGVuLCBkaWUgbWVpc3RlbiBqZWRvY2ggZGVyZW4gdW5taXR0ZWxiYXJlciBFaW5mbHVzeiBhdWYgaWhyZSBEaWNodHVuZy4gVWxqYW5hIFdvbGYgaMOkbHQgZGF6dSBpbiBpaHJlbSBBdWZzYXR6ICpaVSBNRUhSU1BSQUNISUdLRUlUIElNIEdFRElDSFQqIGZlc3QsIGRhc3ogTWVocnNwcmFjaGlna2VpdCAiZWluIMOkc3RoZXRpc2NoZXMsIGtlaW4gYmlvZ3JhZmlzY2hlcyBNb21lbnQiIHNlaSB1bmQgImRhc3MgYXVjaCB2b24gZWluc3ByYWNoaWdlbiBvZGVyIGVpbm11dHRlcnNwcmFjaGlnZW4gQXV0b3I6aW5uZW4gdHJhbnNsaW5ndWFsZSBMaXRlcmF0dXIgZHVyY2ggdmVyc2NoaWVkZW5lIFNjaHJlaWJzdHJhdGVnaWVuIGVyemV1Z3Qgd2VyZGVuIGthbm4sIHVtIGZlc3RnZWbDvGd0ZSBTcHJhY2hvcmRudW5nZW4genUgdmVydW5zaWNoZXJuLiIgW0B3b2xmX2V0eW1vbG9naXNjaGVyXzIwMjEsMTE4XS4gV29sZiBrb21tdCBuaWNodCAtIHNpZSBtZWludCwgaWhyZXMgKmtvY2hhbmllKiB3ZWdlbiB2aWVsZmFjaCB2ZXJtdXRldCBbQHdvbGZfZXR5bW9sb2dpc2NoZXJfMjAyMSw1XSAtIGF1cyBkZW0gcG9sbmlzY2gtdWtyYWluaXNjaGVuIEdyZW56bGFuZCwgc29uZGVybiBhdXMgT3N0YmVybGluLCBoYXQgamVkb2NoIGludGVuc2l2IHJ1c3Npc2NoIHVuZCBlYmVuIGF1Y2ggcG9sbmlzY2ggZ2VsZXJudCAodW5kIGdlbGVidCkgdW5kIHNpY2ggaW4gYWxsZSBTcHJhY2hlbiBiZWdlYmVuLCBkaWUgZsO8ciBzaWUgZnJ1Y2h0YmFyIHdhcmVuOyB6YWhscmVpY2hlIFN0aXBlbmRpZW5hdWZlbnRoYWx0ZSB1bmQgbmljaHQgenVsZXR6dCBpaHIgendpc2NoZW4gTmV3IFlvcmsgdW5kIEJlcmxpbiBwZW5kZWxuZGVzIEFyYmVpdHN3ZXNlbiB6ZXVnZW4gZGF2b24uICAKCiMgd29yawojIyBjb3JwdXMgYXVmYmVyZWl0dW5nCkRhcyBLb3JwdXMsIHdlbGNoZXMgbmFjaCBEaWdpdGFsaXNpZXJ1bmcgZGVyIEJ1Y2h2b3JsYWdlbiBhdXMgZWluZXIgRGF0ZW5iYW5rIGFiZ2VydWZlbiB3aXJkLCBlbnRow6RsdCBgciBsZW5ndGgoZHRhX3NmJGNvbnRlbnQpYCBFaW50csOkZ2UsIG5hY2ggQWJ6dWcgZGVyIEthcGl0ZWzDvGJlcnNjaHJpZnRlbiB1bmQgWml0YXRlIGByIGxlbmd0aChkdGEkY29udGVudCktMWAgRGF0ZW5zw6R0emUgKFRleHRlKSwgZGllIHp1ciBBdXN3ZXJ0dW5nIGhlcmFuZ2V6b2dlbiB3ZXJkZW4ga8O2bm5lbi4KRsO8ciBkaWUgQW5hbHlzZSB3dXJkZSBkYXMgZ2VzYW10ZSAocHVibGl6aWVydGUpIGx5cmlzY2hlIFdlcmsgVWxqYW5hIFdvbGZzLCBiZXN0ZWhlbmQgYXVzLCBpbiBkZXIgUmVpaGVuZm9sZ2UgZGVzIEVyc2NoZWluZW5zOgoKLSBrb2NoYW5pZSwgaWNoIGhhYmUgQnJvdCBnZWthdWZ0IFtAd29sZl9rb2NoYW5pZV8yMDA1XQotIGZhbHNjaGUgZnJldW5kZSBbQHdvbGZfZmFsc2NoZV8yMDA5XQotIG1laW5lIHNjaMO2bnN0ZSBsZW5nZXZpdGNoIFtAd29sZl9tZWluZV8yMDEzXQoKaGVyYW5nZXpvZ2VuLgoKIyMgYmFzaWMgc3RhdGlzdGljcwpgYGB7ciBiYXNpYywgZWNobyA9IEZBTFNFLHdhcm5pbmc9RkFMU0V9Cm1kX3Q8LW1lZGlhbihkdGFfdCR0b2tlbnMpICNkdXJjaHNjaG5pdHRsaWNoZSB0ZXh0bMOkbmdlCm1pbl90PC1taW4oZHRhX3QkdG9rZW5zWzI6bGVuZ3RoKGR0YV90JHRva2VucyldKQptbHg8LXN1YnNldChseHRhYmxlLGx4dGFibGUkbXVsdGk9PSJtdWx0aUxYIikKbG1seDwtbGVuZ3RoKG1seCRseHRvaykKbWx4X3U8LXVuaXF1ZShtbHgkbHh0b2tbMTpsbWx4XSkKdG9rZW5hcnJheTwtZ2V0X3RhcnJheSgpCnRva2VuX25hPC10b2tlbmFycmF5WyFpcy5uYSh0b2tlbmFycmF5KV0KbHRvPC1sZW5ndGgodG9rZW5fbmEpCmx0eTwtbGVuZ3RoKHVuaXF1ZSh0b2tlbl9uYSkpCmBgYAoKV2lyIHdlcmRlbiB2ZXJzdWNoZW4sIGluIGRlciBBcmJlaXQgZWluaWdlIEtlbm56YWhsZW4genUgYmVzdGltbWVuLCBkaWUgY2hhcmFrdGVyaXN0aXNjaCBmw7xyIGRhcyBXZXJrIHNlaW4gc29sbGVuLiBCYXNpcyBzaW5kIGhpZXIgU3RhdGlzdGlrZW4gw7xiZXIgV29ydGzDpG5nZW4gdW5kIC1mcmVxdWVuemVuLCBEaXN0cmlidXRpb24gbXVsdGlsaW5ndWFsZXIgRWxlbWVudGUgw7xiZXIgZGFzIEtvcnB1cyB1bmQgQW5uw6RoZXJ1bmdzd2VydGUgenVyIEJlc3RpbW11bmcgZGVzICpzZW50aW1lbnQqLiBEaWUgWmFobGVuIHdlcmRlbiBhYnNvbHV0IHVuZC9vZGVyIHJlbGF0aXYgYW5nZWdlYmVuOyBhYnNvbHV0IG1laW50IGhpZXIgZGllIGtvbmtyZXRlIEJlemllaHVuZyB6dSBlaW5lciBQb3NpdGlvbiBpbSBLb3JwdXMsIHJlbGF0aXYgbWVpbnQgamV3ZWlscyBkaWUgaW5kZXhpa2FsaXNpZXJ0ZSwgYXVmIGVpbmVyIEdlc2FtdGhlaXQgdi5ILiBhbmdlbm9tbWVuZSBQb3NpdGlvbiBvZGVyIFJlbGF0aW9uLiBEaWVzZSBSZWxhdGl2aWVydW5nIGVybcO2Z2xpY2h0IGVpbmUgZ2xlaWNoZsO2cm1pZ2UgVmlzdWFsaXNpZXJ1bmcgZGVyIERhdGVuIGluIGdsYXR0ZW4gRnJlcXVlbnprdXJ2ZW4sIHVtIGRpZSBWZXJow6RsdG5pc3NlIHNjaGVtYXRpc2NoIGFienViaWxkZW4uIChadXIgQmVyZWNobnVuZyBkZXIgRm91cmllci10cmFuc2Zvcm1pZXJ0ZW4gKEZGVCkgRnJlcXVlbnplbiBjZi4gW0Bqb2NrZXJzX3JldmVhbGluZ18yMDE1XShodHRwczovL3d3dy5tYXR0aGV3am9ja2Vycy5uZXQvMjAxNS8wMi8wMi9zeXV6aGV0LykpCgojIyMgZ3JvdW5kIHRydXRoCkRpZSBgciBsY2AgVGV4dGUgKEx5cmlrIHVuZCBseXJpc2NoZSBvZGVyIGV4cGVyaW1lbnRlbGxlIFByb3NhKSBoYWJlbiBlaW5lbiBVbWZhbmcgdm9uIGByIGx0b2AgV8O2cnRlcm4gKHRva2VucyksIGRpZSBzaWNoIGluIGByIGx0eWAgZGlzdGluY3QgdHlwZXMgZWludGVpbGVuIGxhc3NlbiwgZGllIHR5cGUvdG9rZW4gcmF0aW8sIGVpbiBJbmRpa2F0b3IgZsO8ciAqbGV4aWNhbCBkaXZlcnNpdHkqLCBiZXRyw6RndCBkZW1uYWNoIGByIGx0eS9sdG9gLiBEaWUgZHVyY2hzY2huaXR0bGljaGUgVGV4dGzDpG5nZSAobWVkaWFuKSBiZXRyw6RndCBgciBtZF90YCBXw7ZydGVyLiBXaXIgaGFiZW4gbm9jaCBrZWluZSBWZXJnbGVpY2hzd2VydGUsIGRpZSBzaW5udm9sbCB3w6RyZW4uLi4KCiMjIyBtdWx0aUxYCkRpZSBtdWx0aWxpbmd1YWxlbiBFbGVtZW50ZSBkZXMgS29ycHVzIChpbnNnZXNhbXQgYHIgbG1seGAgdG9rZW5zKSBoYWJlbiBlaW5lbiBBbnRlaWwgdm9uIGByIHJvdW5kKGxlbmd0aChtbHhfdSkvbHR5KjEwMClgJSBhbiBkZW4gdHlwZXMuCk1pdCBkZXIgVGV4dG1hdHJpeCAoY2YuIFRhYmxlIFxAcmVmKHRhYjp0ZXh0LW1hdHJpeCkpIGzDpHN6dCBzaWNoIG5vY2ggd2VpdGVyIHJlY2huZW4uCgpgYGB7ciBseC1tYXRjaGVzLCBlY2hvPUYsZmlnLmNhcD0ibXVsdGlsaW5ndWFsIGVsZW1lbnRzIG92ZXIgY29ycHVzIix3YXJuaW5nPUZBTFNFfQpzZW50X2dsb2JhbF9mPC1nZXRfdHJhbnNmb3JtZWRfdmFsdWVzKHNlbnRfZ2xvYmFsKQpwbG90KGdldF9seG1hdGNoZXMoKSx0eXBlID0gImgiLHhsYWI9InRleHQgY29ycHVzIix5bGFiPSJvY2N1cmVuY2VzIiwgbWFpbj0ib2NjdXJlbmNlcyBvZiBub24gZ2VybWFuIHdvcmRzIikKYGBgCgojIyMgc2ltaWxhcml0aWVzCmBgYHtyIHRleHQtbWF0cml4LCBlY2hvID0gRix3YXJuaW5nPUZBTFNFfQprbml0cjo6a2FibGUod29sZm1hdHJpeFsxOjEwLCAxOjhdLCBjYXB0aW9uID0gIipzaW1wbGVzdCBtYXRyaXggb2YgdGV4dCBiZWdpbm5pbmdzKiIpCmVuZDwtNTAKI3R5cGVhcnJheSBudW1iZXJzOgptYXh0eTwtd2hpY2gubWF4KHR5cGVhcnJheV9mKQptYXhjaDwtd2hpY2gubWF4KGNoYXJhcnJheV9mKQptYXhjaF9uPC1tYXgoY2hhcmFycmF5X2YpCm1heGNoMDwtbWF4Y2gtNQptYXhjaDE8LW1heGNoKzUKbWRjaDwtbWVkaWFuKGNoYXJhcnJheV9mKQptZHA8LWdyZXAocm91bmQobWRjaCwyKSxjaGFyYXJyYXlfZikKbWluY2hfbjwtbWluKGNoYXJhcnJheV9mW21kcF0pCm1heDI8LXdoaWNoLm1heChjaGFyYXJyYXlfZlttYXhjaDErNTpsZW5ndGgoY2hhcmFycmF5X2YpXSkKI21heDM8LWxlbmd0aChjaGFyYXJyYXlfZiktbWF4Y2gxKzUKbWF4MzwtbWF4Y2gxKzUrbWF4MgpgYGAKClp1bSBCZWlzcGllbCBsYXNzZW4gc2ljaCBkaWUgV29ydGdsZWljaHVuZ2VuIHZpc3VhbGlzaWVyZW4sIGRpZSBhbiBiZXN0aW1tdGVuIFBvc2l0aW9uZW4gZGVzIFRleHRlcyBhdWZzY2hlaW5lbi4gRGllIEjDtmhlbiBpbiBkZXIgZm9sZ2VuZGVuIEdyYXBoaWsgbWFya2llcmVuIHJlbGF0aXZlIChGb3VyaWVyLXRyYW5zZm9ybWllcnRlKSBXb3J0cG9zaXRpb25lbiwgYW4gZGVuZW4gdm9uIFdvbGYgZGllICoqd2VuaWdzdGVuKiogYW5hbG9nZW4gV8O2cnRlciB2ZXJ3ZW5kZXQgd3VyZGVuLiBFcyBsw6RzenQgc2ljaCBlcmtlbm5lbiwgZGFzeiBlaW4gVGV4dCBtZWlzdCBtaXQgZGVuc2VsYmVuIFfDtnJ0ZXJuIGFuZsOkbmd0IChiYWlzc2UpLCBkaWUgaW1tZXIgdmVyc2NoaWVkZW5lciB3ZXJkZW4sIHVtIHNpY2ggYmVpIGRlciBIw6RsZnRlIGRlcyBUZXh0ZXMgw7xiZXIgZWluZSBsYW5nZSBTdHJlY2tlIHp1IGdsZWljaGVuIHVuZCBhYiA2MCUgc3BydW5naGFmdCB6dSBkaXZlcmdpZXJlbiBiaXMgc2llIHVtIGByIG1heHR5YCUgZWluZW4gcGVhayAoaGF1c3NlKSBlcnJlaWNoZW4gYW4gVmVyc2NoaWVkZW5oZWl0LgoKYGBge3IgdGV4dC1zaW0tZ3IsZmlnLmNhcD0iZGlzdGluY3RuZXNzIG9mIHdvcmQgcG9zaXRpb25zIiwgZWNobyA9IEYsd2FybmluZz1GQUxTRX0KI2VuZDwtNTAKI3Bsb3QodHlwZWFycmF5WzE6NTBdLHR5cGU9ImgiLHhsYWIgPSBwYXN0ZTAoImZpcnN0ICIsIGVuZCwiIHdvcmRzIG9mIHRleHRzIikseWxhYj0iY291bnQgb2YgZGlzdGluY3QgdHlwZXMiKQojc2NhdHRlci5zbW9vdGgoMTplbmQsdHlwZWFycmF5WzE6ZW5kXSwuMSwuMSx0eXBlPSJoIixmYW1pbHkgPSAiZ2F1c3NpYW4iLHlsYWI9ImNvdW50IG9mIGRpc3RpbmN0IHR5cGVzIix4bGFiID0gcGFzdGUwKCJmaXJzdCAiLCBlbmQsIiB3b3JkcyBvZiB0ZXh0cyIpKQoKc2NhdHRlci5zbW9vdGgoMTpsZW5ndGgodHlwZWFycmF5X2YpLHR5cGVhcnJheV9mLC4xLC4xLHR5cGU9ImgiLGZhbWlseSA9ICJnYXVzc2lhbiIseWxhYj0ibWVhbiBvZiBkaXN0aW5jdCB0eXBlcyIseGxhYiA9ICJyZWxhdGl2ZSBwb3NpdGlvbiBvZiB3b3JkcyBpbiB0ZXh0cyIpCgpgYGAKCkVpbmUgd2VpdGVyaGluIHNjaMO2bmUgR3JhcGhpayBlbnRzdGVodCwgd2VubiBtYW4gZGllIE1hdHJpeCBkZXIgWmVpY2hlbmFuemFobCDDvGJlciBkaWUgR2VzYW10aGVpdCBkZXIgV8O2cnRlciB2aXN1YWxpc2llcnQuIEhpZXIgemVpZ3Qgc2ljaCwgZGFzeiBlaW4gVGV4dCB6d2lzY2hlbiBgciBtYXhjaDBgLWByIG1heGNoMWAlIGRpZSBsw6RuZ3N0ZW4gV8O2cnRlciAobWVhbjogYHIgcm91bmQobWF4Y2hfbiwyKWAgY2hhcmFjdGVycykgZW50aMOkbHQsIGRpZXNlIHp3aXNjaGVuIGByIG1kcFsxXWAgdW5kIGByIG1kcFsyXWAlIGvDvHJ6ZXIgd2VyZGVuIGJpc2hpbiB6dSBgciByb3VuZChtaW5jaF9uLDIpYCBaZWljaGVuIHVtIGJlaSBgciBtYXgzYCUgZWluZW4gZXJuZXV0ZW4gcGVhayBpbiBkZXIgWmVpY2hlbmFuemFobCAobWVhbjogYHIgcm91bmQoY2hhcmFycmF5X2ZbbWF4M10sMilgIGNoYXJhY3RlcnMpIHp1IGVycmVpY2hlbi4KCmBgYHtyIHdjLGZpZy5jYXA9ImNoYXJhY3RlcnMgcGVyIHBvc2l0aW9uIiwgZWNobyA9IEYsd2FybmluZz1GQUxTRX0KI2VuZDwtNTAKc2NhdHRlci5zbW9vdGgoMTpsZW5ndGgoY2hhcmFycmF5X2YpLGNoYXJhcnJheV9mLC4xLC4xLHR5cGU9ImgiLGZhbWlseSA9ICJnYXVzc2lhbiIseWxhYj0ibWVhbiBjb3VudCBvZiBjaGFyYWN0ZXJzIix4bGFiID0gInJlbGF0aXZlIHBvc2l0aW9uIG9mIHdvcmRzIGluIHRleHRzIikKCiNpbWFnZSh3Yyx4YXh0PSJuIix5YXh0PSJuIix4bGFiPSJ0ZXh0cG9zaXRpb24gaW4gY29ycHVzIix5bGFiPSJ3b3JkcG9zaXRpb24gaW4gI3RleHQiKQpgYGAKCiMjIHNlbnRpbWVudCBhbmFseXNpcwpGw7xyIGplZGVuIGVpbnplbG5lbiBUZXh0IGthbm4gZWluIFdlcnQgYmVzdGltbXQgd2VyZGVuLCBkZXIgQXVzc2FnZW4gZGFyw7xiZXIgenVsaWVzemUsIHdvIGltIFNwZWt0cnVtIHBvc2l0aXZlL25lZ2F0aXZlIHNlbnRpbWVudCBzaWNoIGRpZXNlciB2ZXJvcnRlbiBsw6RzenQuCkRpZSBhYnNvbHV0ZW4gKnNlbnRpbWVudCB2YWx1ZXMqIHdlcmRlbiB3ZWl0ZXJoaW4gZHVyY2ggRm91cmllci1UcmFuc2Zvcm1hdGlvbiBhdWYgZGllIEdlc2FtdGhlaXQgZGVzIEtvcnB1cyBwcm9qaXppZXJ0LCB1bSBlaW5lIGdsYXR0ZSwgdm9uIGRlciBhYnNvbHV0ZW4gUG9zaXRpb24gdW5hYmjDpG5naWdlIERhcnN0ZWxsdW5nIHp1IGVybcO2Z2xpY2hlbi4gKGNmLiBGaWd1cmUgXEByZWYoZmlnOnNlbnQtZnJlcSkpLgpXZWxjaGUgQXVzc2FnZW4gc2ljaCBhdXMgZGllc2VuIEVya2VubnRuaXNzZW4gYWJsZWl0ZW4gbGFzc2VuIHNvbGxlbiwgaXN0IG1pciBub2NoIG5pY2h0IGdhbnoga2xhci4gSSB3aWxsIGVsYWJvcmF0ZSBvbiB0aGF0LgoKIyMjIGluIHdvcmRzCnN1bW1hcnk6CmBgYHtyIGVjaG89RixldmFsPVRSVUUsIGVjaG89RkFMU0UsIGNvbGxhcHNlPVRSVUUsIHdhcm5pbmc9RkFMU0UsbWVzc2FnZT1GQUxTRX0KZXhjPC0zCiMgbWZ3X2R0YTwtbGlzdCgpCiMgZm9yIChrIGluIDI6IGxlbmd0aChjaGFwdGVyX2V4KSl7CiMgICAKIyAKIyBtZndfZHRhW1trXV08LW1mdyhkdGEsaykKIyB9CgpwcmludCAobWZ3X2R0YVtbZXhjXV0pCiNrbml0cjo6a2FibGUobWZ3X2R0YSw1LDUpCmBgYApgYGB7Y3NzIGVjaG89Rn0KcHJlIHttYXgtaGVpZ2h0OiA0MDBweDt9CiNtb3N0LXByb2JhYmxlLXRleHQgcCB7Zm9udC1mYW1pbHk6IENvdXJpZXI7fQpgYGAKClp1bSBCZWlzcGllbDogRGllIGjDtmNoc3RlbiAqc2VudGltZW50KiBXZXJ0ZSwgaGllciBpbiBbY2hhcHRlcjpdIGBgciBtZndfZHRhW1tleGNdXSRtYXgkY2hhcHRlcmBgLCBsYXNzZW4gc2ljaCBpbiBbdGV4dDpdIGBgciBtZndfZHRhW1tleGNdXSRtYXgkaGVhZGBgIGZpbmRlbi4gRGllICptb3N0IGZyZXF1ZW50IHdvcmRzKiBkaWVzZXMgQWJzY2huaXR0cyBzaW5kIGBgciBuYW1lcyhtZndfZHRhW1tleGNdXSRtYXgkd29yZHMpYGAsIGRpZSBuaWVkcmlnc3RlbiBmaW5kZW4gc2ljaCBpbSBUZXh0IGBgciBtZndfZHRhW1tleGNdXSRtaW4kaGVhZGBgIG1pdCBgYHIgbmFtZXMobWZ3X2R0YVtbZXhjXV0kbWluJHdvcmRzKWBgLgoKIyMjIHZpc3VhbGlzYXRpb24KYGBge3IgZXZhbD1UUlVFLCBlY2hvPUZBTFNFLCBjb2xsYXBzZT1UUlVFLCB3YXJuaW5nPUZBTFNFLG1lc3NhZ2U9RkFMU0V9CiNjYWxscyBtaXJhY2xlIGZ1bmN0aW9uIGZyb20gZXh0ZXJuYWwgc2NyaXB0OgojYm9vazwtMwojY2hhcHRlcjwtMwojcGxvdF9hYnM8LTAKI3RleHQ8LTIKI2R0YXRhcmdldDwtcGxvdHNlbnRpbWVudChkdGF0eHQsYm9vayxjaGFwdGVyLHBsb3RfYWJzLDMpICNBUkc6IChzZXQsYm9vayxjaGFwdGVyLGFic29sdXRlKQojb3V0IGR0YV90PC1nZXRfdHlwZXMoZHRhLDEpCmxlPC1kb19zZW50aW1lbnQoZHRhX3QpCiMgbWZ3X2R0YTwtbGlzdCgpCiMgZm9yIChrIGluIDI6IGxlbmd0aChjaGFwdGVyX2V4KSl7CiMgICAKIyAKIyBtZndfZHRhW1trXV08LW1mdyhkdGEsaykKIyB9CiNtZndfZHRhW1szXV0kbWF4JGlkCmBgYAoKYGBge3Igc2VudC1hYnMsIGZpZy5jYXA9ImFic29sdXRlICpzZW50aW1lbnQgdmFsdWVzKiDDvGJlciBkYXMgZ2VzYW10ZSBUZXh0a29ycHVzIixlY2hvPUZBTFNFfQogIyBzZW50MjwtYyhhMSxhMixhMykgI3VudHJhbnNmb3JtZWQgc2VudGltZW50LCBhYnNvbHV0ZQogIHNjYXR0ZXIuc21vb3RoKDE6bGVuZ3RoKGxlJHNlbnRpbWVudCRjcHRfczIpLGxlJHNlbnRpbWVudCRjcHRfczIsLjEsLjEsdHlwZT0iaCIsZmFtaWx5ID0gImdhdXNzaWFuIix5bGFiPSJhYnNvbHV0ZSBzZW50aW1lbnQgdmF1bGVzIix4bGFiPSJ0ZXh0IGNvcnB1cyIsbWFpbj0ic2VudGltZW50IG92ZXIgdGV4dHMiKQpgYGAKCmBgYHtyIHNlbnQta29jaCwgZmlnLmNhcD0iYWJzb2x1dGUgKnNlbnRpbWVudCB2YWx1ZXMqIMO8YmVyICprb2NoYW5pZSBpY2ggaGFiZSBicm90IGdla2F1ZnQqIixlY2hvPUZBTFNFfQogIHNjYXR0ZXIuc21vb3RoKDE6bGVuZ3RoKGxlJHNlbnRpbWVudCRhMSksbGUkc2VudGltZW50JGExLC4xLC4xLHR5cGU9ImgiLGZhbWlseSA9ICJnYXVzc2lhbiIseWxhYj0iYWJzb2x1dGUgc2VudGltZW50IHZhdWxlcyIseGxhYj0idGV4dDoga29jaGFuaWUiLG1haW49InNlbnRpbWVudCBvdmVyIHRleHRzIikKYGBgCgpgYGB7ciBzZW50LWZmLCBmaWcuY2FwPSJhYnNvbHV0ZSAqc2VudGltZW50IHZhbHVlcyogw7xiZXIgKmZhbHNjaGUgZnJldW5kZSoiLGVjaG89RkFMU0V9CiAgc2NhdHRlci5zbW9vdGgoMTpsZW5ndGgobGUkc2VudGltZW50JGEyKSxsZSRzZW50aW1lbnQkYTIsLjEsLjEsdHlwZT0iaCIsZmFtaWx5ID0gImdhdXNzaWFuIix5bGFiPSJhYnNvbHV0ZSBzZW50aW1lbnQgdmF1bGVzIix4bGFiPSJ0ZXh0OiBGRiIsbWFpbj0ic2VudGltZW50IG92ZXIgdGV4dHMiKQpgYGAKCmBgYHtyIHNlbnQtbGVuZywgZmlnLmNhcD0iYWJzb2x1dGUgKnNlbnRpbWVudCB2YWx1ZXMqIMO8YmVyICptZWluZSBzY2jDtm5zdGUgbGVuZ2V2aXRjaCoiLGVjaG89RkFMU0V9CiAgc2NhdHRlci5zbW9vdGgoMTpsZW5ndGgobGUkc2VudGltZW50JGEzKSxsZSRzZW50aW1lbnQkYTMsLjEsLjEsdHlwZT0iaCIsZmFtaWx5ID0gImdhdXNzaWFuIix5bGFiPSJhYnNvbHV0ZSBzZW50aW1lbnQgdmF1bGVzIix4bGFiPSJ0ZXh0OiBsZW5nZXZpdGNoIixtYWluPSJzZW50aW1lbnQgb3ZlciB0ZXh0cyIpCiMgIHNlbnQzPC1nZXRfdHJhbnNmb3JtZWRfdmFsdWVzKHNlbnQyKQpgYGAKCldpciBzZWhlbiBpbiBkZW4gZnJlcXVlbnphbmFseXNpZXJ0ZW4gR3JhcGhpa2VuLCBkYXN6IHNpY2ggZGllIHJlbGF0aXZlIFZlcnRlaWx1bmcgZGVyIHNlbnRpbWVudCB2YWx1ZXMgw7xiZXIgZGllIELDvGNoZXIgaW4gZGVyIFRlbmRlbnogdW50ZXJzY2hlaWRldC4gV8OkaHJlbmQgaW4gKmtvY2hhbmllKiB1bmQgKmxlbmdldml0Y2gqIHNjaG9uIHp1IEJlZ2lubiBIw7ZoZW4gdmVyemVpY2huZXQgc2luZCwgZGllIFdlcnRlIGRhbm4genVyIEJ1Y2htaXR0ZSBoaW4gc2lua2VuLCB6ZWlndCBzaWNoIGJlaSAqRkYqIGVpbiBlcnN0ZXIgV2VjaHNlbCB2b24gbmVnYXRpdiB6dSBwb3NpdGl2IHNjaG9uIGltIGVyc3RlbiBEcml0dGVsLiBEaWUgU3RpbW11bmcgYWxsZXIgZHJlaSBCw7xjaGVyIGlzdCBpbiBkZXIgTWl0dGUgZ2xlaWNoIG5lZ2F0aXYgKGJld2VydGV0KSwgaW4gKmtvY2hhbmllKiBhYmVyIHNjaG9uIHdpZWRlciBhdWZzdGVpZ2VuZCwgKmZhbHNjaGUgZnJldW5kZSogd2Vpc3QgZGllIGdyw7ZzenRlbiBTY2h3YW5rdW5nZW4gYXVmLiAKCmBgYHtyIHNlbnQtY29tcCxmaWcuY2FwPSJyZWxhdGl2ZSBzZW50aW1lbnQgdmFsdWVzIHNpbmdsZWQiLGVjaG89RkFMU0V9CnBhcihuZXc9RikKcGxvdChsZSRzZW50aW1lbnQkYTFpLHR5cGUgPSAiaCIsY29sPTQseWxhYiA9ICJzZW50aW1lbnQgZnJlcXVlbmNpZXMiLHhsYWI9ImJsdWU6IGtvY2hhbmllLCByZWQ6IEZGLCB5ZWxsb3c6IGxlbmdldml0Y2giLG1haW49InNlbnRpbWVudCBkaXN0cmlidXRpb24gb3ZlciBib29rIikKcGFyKG5ldz1UKSAjcmVkCnBsb3QobGUkc2VudGltZW50JGEyaSx0eXBlID0gImgiLGNvbD0yLHhheHQ9Im4iLHlheHQ9Im4iLGFubiA9IEYpCnBhcihuZXc9VCkgI2dyZWVuCnBsb3QobGUkc2VudGltZW50JGEzaSx0eXBlID0gImgiLGNvbD03LHhheHQ9Im4iLHlheHQ9Im4iLGFubiA9IEYpICNibHVlCmBgYAoKYGBge3Igc2VudC1hYnMtY3B0LCBmaWcuY2FwPSJhYnNvbHV0ZSAqc2VudGltZW50IHZhbHVlcyogb3ZlciBjb3JwdXMiLGVjaG89RkFMU0V9CmRmPC1zdWJzZXQoZHRhX3QsZHRhX3QkcGFnZSE9Im51bGwiKQogIHA8LWdncGxvdChkZiwgYWVzKDE6bGVuZ3RoKHNlbnRpbWVudCksIHNlbnRpbWVudCwgY29sb3VyID0gYm9vaykpICsgCiAgICBnZW9tX2xpbmUoKQogIHAgKyAgbGFicyh4PSJjb3JwdXMiLCB5PSJzZW50aW1lbnQgYWJzb2x1dGUiLCB0aXRsZT0ic2VudGltZW50IG92ZXIgdGV4dHMiKQpgYGAKCkluICprb2NoYW5pZSogd2Vpc2VuIGRpZSBXZXJ0ZSBkaWUgbmllZHJpZ3N0ZSwgaW4gKmZhbHNjaGUgZnJldW5kZSogZGllIGjDtmNoc3RlIFZhcmlhbnogYXVmLiAKCmBgYHtyIHNlbnQtZnJlcSwgZmlnLmNhcD0iZnJlcXVlbnphbmFseXNpZXJ0ZSAoRm91cmllcikgKnNlbnRpbWVudCB2YWx1ZXMqIMO8YmVyIEtvcnB1cyIsZWNobz1GQUxTRX0KICBwbG90KGxlJHNlbnRpbWVudCRjcHRfczEsdHlwZSA9ICJoIixjb2w9Mix5bGFiID0gInNlbnRpbWVudCBmcmVxdWVuY2llcyIseGxhYj0iY29ycHVzIixtYWluPSJzZW50aW1lbnQgb3ZlciB0ZXh0cyIpCmBgYAoKYGBge3Igc2VudC1mci1jcHQsIGZpZy5jYXA9ImZyZXF1ZW5jeSBhbmFseXNpcyIgLGVjaG89RkFMU0V9CiAgcGxvdChsZSRzZW50aW1lbnQkY3B0X3MzLHR5cGUgPSAiaCIsY29sPTIseWxhYiA9ICJzZW50aW1lbnQgZnJlcXVlbmNpZXMiLHhsYWI9ImNvcnB1cyBhZ2dsb21lcmF0ZWQiLG1haW49InNlbnRpbWVudCBhbmFseXNpcyBvdmVyIHRleHRzIikKYGBgCgojIyMgZGVwZW5kZW5jaWVzCk1pdCBkZXIgUmVncmVzc2lvbnNhbmFseXNlIGRlcyAqUiBsbWU0IHBhY2thZ2UqIFtAYmF0ZXNfZml0dGluZ18yMDE1XSBsYXNzZW4gc2ljaCBoaWVyIEFiaMOkbmdpZ2tlaXRlbiAoS29ycmVsYXRpb25lbikgZGVyICpzZW50aW1lbnQgdmFsdWVzKiB2b24gdmVyc2NoaWVkZW5lbiBGYWt0b3JlbiAoY2hhcHRlciwgYm9vaywgbXVsdGlsaW5ndWFsIGVsZW1lbnRzKSBhdWZ6ZWlnZW4uCgojIyMjIGJvb2svY2hhcHRlciBkZXBlbmRlbmN5ICAgCnN1bW1hcnk6CgpgYGB7ciBzdW0tbG1lciwgZWNobz1GQUxTRX0KcHJpbnQobGUkbG0kc3VtKQpgYGAKCmBgYHtyIHNlbnQtbG0xLCBmaWcuY2FwPSJsaW5lYXIgcmVncmVzc2lvbiBvZiBzZW50aW1lbnQgZGVwZW5kZW5jaWVzLCBhYnNvbHV0ZSIsZWNobz1GQUxTRX0KICBzY2F0dGVyLnNtb290aCgxOmxlbmd0aChsZSRsbSRzdW0kcmVzaWR1YWxzKSxsZSRsbSRzdW0kcmVzaWR1YWxzLC4xLC4xLHR5cGU9ImgiLGZhbWlseSA9ICJnYXVzc2lhbiIseWxhYj0iZGVwZW5kZW5jaWVzOiBsbWVyIHNlbnRpbWVudCByZXNpZHVhbHMiLHhsYWI9InRleHQgY29ycHVzIixtYWluPSJzZW50aW1lbnQgYm9vay9jaGFwdGVyIGRlcGVuZGVuY3kiKQpkZXBtYXg8LXdoaWNoLm1heChsZSRsbSRzdW0kcmVzaWR1YWxzKQpkZXBtaW48LXdoaWNoLm1pbihsZSRsbSRzdW0kcmVzaWR1YWxzKQpkZXBtYXhyPC1yb3VuZChtYXgobGUkbG0kc2NhbGVkKSkKZGVwbWlucjwtcm91bmQobWluKGxlJGxtJHNjYWxlZCkpCgojZHRhX3QkcGhlYWRbZGVwbWluXQojZGVwbWF4CiNsZW5ndGgobGUkbG0kc3VtJHJlc2lkdWFscykKYGBgCgpFcyBpc3QgenUgemVpZ2VuLCBkYXN6IGRpZSBBYmjDpG5naWdrZWl0IGR1cmNoYXVzIHZhcmlpZXJ0LiBEaWUgcmVsYXRpdmVuIEtvcnJlbGF0aW9uc3dlcnRlIHNjaHdhbmtlbiB6d2lzY2hlbiBgciBkZXBtaW5yYCB1bmQgYHIgZGVwbWF4cmAgKGJlaSBmKHgpPXgvMTAwKSwgendpc2NoZW4gNDAtODAlIGzDpHN6dCBzaWNoIGdyw7ZzemVyZSBBYmjDpG5naWdrZWl0IGJlb2JhY2h0ZW4sIGRoLiBoaWVyIHNpbmQgZGllIHNlbnRpbWVudCB2YWx1ZXMgYW0gc3TDpHJrc3RlbiB2b20gS2FwaXRlbCBiZWVpbmZsdXN6dCwgYmVpc3BpZWxoYWZ0IGJlaW0gVGV4dFtgciBkZXBtYXhgOl0gIGByIGR0YV90JHBoZWFkW2RlcG1heF1gLCBhbSB3ZW5pZ3N0ZW4gYmVpbSBUZXh0W2ByIGRlcG1pbmA6XSAgYHIgZHRhX3QkcGhlYWRbZGVwbWluXWAuIChJbiBkZXIgUmVncmVzc2lvbnNhbmFseXNlIHd1cmRlbiBWZXLDpG5kZXJ1bmdlbiBkZXIgV2VydGUgKFZhcmlhYmxlbikgYHNlbnRpbWVudGAgZGVyIFRleHRlIGF1ZiBlaW5lbiBadXNhbW1lbmhhbmcgbWl0IEJ1Y2ggdW5kIEthcGl0ZWwgZGVyIGpld2VpbGlnZW4gTWVzc3VuZyBnZXByw7xmdCwgZGguIGJlc3RpbW10LCBvYiBCdWNoIHVuZC9vZGVyIEthcGl0ZWwgZWluZW4gRWluZmx1c3ogYXVmIGRlbiBXZXJ0IGhhYmVuLikgICAgCgpgYGB7ciBzZW50LWxtLWZyLCBmaWcuY2FwPSJsaW5lYXIgcmVncmVzc2lvbiBvZiBzZW50aW1lbnQgZGVwZW5kZW5jaWVzLCByZWxhdGl2ZSIsZWNobz1GQUxTRX0KICBwbG90KGxlJGxtJHNjYWxlZCx0eXBlID0gImgiLGNvbD0yLHlsYWIgPSAic2VudGltZW50IGZyZXF1ZW5jaWVzIGF1ZiAxMDAlIix4bGFiPSJjb3JwdXMiLG1haW49InNlbnRpbWVudCBhbmFseXNpcyBvdmVyIHRleHRzIikKYGBgCgojIyMjIG11bHRpTFggZGVwZW5kZW5jeQpXZWl0ZXJoaW4ga8O2bm5lbiB3aXIgdmVyc3VjaGVuLCBlaW5lIEFiaMOkbmdpZ2tlaXQgZGVyIHNlbnRpbWVudCB2YWx1ZXMgdm9uIGRlciBWZXJ3ZW5kdW5nIG11bHRpbGluZ3VhbGVyIEVsZW1lbnRlIGF1Znp1emVpZ2VuLiBEaWUgdmVyZGljaHRldGVuIHNjaHdhcnplbiBCYWxrZW4gKGNmLiBGaWd1cmUgXEByZWYoZmlnOmx4LW1hdGNoZXMpKSBrb3JyZWxpZXJlbiBoaWVyIG1pdCBkZXIgcm90ZW4gTGluaWUgZGVyIFN0aW1tdW5nc3dlcnRlLCB3YXMgZWluZSBBYmjDpG5naWdrZWl0IHZlcm11dGVuIGzDpHN6dC4KCmBgYHtyIGx4LXNlbnQtcHJvamVjdGlvbiwgZWNobz1GLGZpZy5jYXA9ImFic29sdXRlIHBvc2l0aW9uZWQgbXVsdGlsaW5ndWFsIGVsZW1lbnRzIG92ZXIgc2VudGltZW50Iix3YXJuaW5nPUZBTFNFfQpzZW50X2dsb2JhbF9mPC1nZXRfdHJhbnNmb3JtZWRfdmFsdWVzKHNlbnRfZ2xvYmFsKQpwbG90KGdldF9seG1hdGNoZXMoKSx0eXBlID0gImgiLHhsYWI9InRleHQgY29ycHVzIix5bGFiPSJvY2N1cmVuY2VzIixtYWluPSJzZW50aW1lbnQvbGFuZ3VhZ2UgY29ycmVsYXRpb24iKQpwYXIobmV3PVQpCnBsb3Qoc2VudF9nbG9iYWxfZix0eXBlID0gImwiLGNvbD0yLHhheHQ9Im4iLHlheHQ9Im4iLGFubiA9IEYpCgojc2NhdHRlci5zbW9vdGgoMTpsZW5ndGgoc2VudF9nbG9iYWwpLHNlbnRfZ2xvYmFsLC4xLC4xLHR5cGU9ImwiLGZhbWlseSA9ICJnYXVzc2lhbiIsY29sPTIseGF4dD0ibiIseWF4dD0ibiIsYW5uID0gRikKYGBgCgpgYGB7ciBseC1zZW50LXByb2plY3Rpb24tZiwgZWNobz1GLGZpZy5jYXA9InBlcmNlbnRhZ2Ugb2YgbXVsdGlsaW5ndWFsIGVsZW1lbnRzIG92ZXIgc2VudGltZW50Iiwgd2FybmluZz1GQUxTRX0Kc2VudF9nbG9iYWxfZjwtZ2V0X3RyYW5zZm9ybWVkX3ZhbHVlcyhzZW50X2dsb2JhbCkgI2dsb2JhbCBzZW50aW1lbnQgdmFsdWVzLCByZWxhdGl2ZQojZHRhX3QkbHhwWzFdPC0wCmx4cF9mPC1nZXRfdHJhbnNmb3JtZWRfdmFsdWVzKGR0YV90JGx4cCkgIwp4MTwtbWF4KGR0YV90JGx4cCkKeDI8LW1heChseHBfZikKeDM8LXgxL3gyCiN4Mip4MwpseHBfZl9wPC1seHBfZip4MwojbHhwbWF0Y2hlcwojcGxvdChseHBtYXRjaGVzLHR5cGUgPSAiaCIpCiNwbG90KGx4cF9mLHR5cGU9ImgiKQpwbG90KGx4cF9mX3AsdHlwZSA9ICJoIix4bGFiPSJ0ZXh0IGNvcnB1cyIseWxhYj0ib2NjdXJlbmNlcyBwZXJjZW50YWdlICUiLG1haW49InNlbnRpbWVudC9sYW5ndWFnZSBjb3JyZWxhdGlvbiIpCnBhcihuZXc9VCkKcGxvdChzZW50X2dsb2JhbF9mLHR5cGUgPSAibCIsY29sPTIseGF4dD0ibiIseWF4dD0ibiIsYW5uID0gRikKCiNzY2F0dGVyLnNtb290aCgxOmxlbmd0aChzZW50X2dsb2JhbCksc2VudF9nbG9iYWwsLjEsLjEsdHlwZT0ibCIsZmFtaWx5ID0gImdhdXNzaWFuIixjb2w9Mix4YXh0PSJuIix5YXh0PSJuIixhbm4gPSBGKQpgYGAKCnN1bW1hcnk6CmBgYHtyIHN1bS1sbWVyMiwgZWNobz1GQUxTRSwgd2FybmluZz1GQUxTRX0KcHJpbnQobG1zKQojIGxtIGV2YWwgZm9yIHJvdyg1KT1seHAKcjwtNQpybmc8LTI6NApnZXRfbG1lcjwtZnVuY3Rpb24ocixybmcpewpjMDwtcm5nWzFdLXJuZ1sxXSsxCmxtbWF4MTwtd2hpY2gubWF4KGxtcyR2Y292W3Iscm5nXSkKI2xtcyR2Y292W3Iscm5nXQpsbW1heDwtbG1zJHZjb3ZbcixsbW1heDErYzBdCmxtbWluMTwtd2hpY2gubWluKGxtcyR2Y292W3Iscm5nXSkKbG1taW48LWxtcyR2Y292W3IsbG1taW4xK2MwXQpjbnNtYXg8LWNvbG5hbWVzKGxtcyR2Y292KVtsbW1heDErYzBdCmNuc21pbjwtY29sbmFtZXMobG1zJHZjb3YpW2xtbWluMStjMF0KY2luPC1tYXRjaChybmcsYyhsbW1heDErYzAsbG1taW4xK2MwKSkKcG1lZDwtcm5nW2lzLm5hKGNpbildCmNuc21lZDwtY29sbmFtZXMobG1zJHZjb3YpW3BtZWRdCiNjbnMzPC1jb2xuYW1lcyhsbXMkdmNvdilbM10KI2NuczQ8LWNvbG5hbWVzKGxtcyR2Y292KVs0XQpsbWRpZjE8LShsbXMkdmNvdltyLGxtbWF4MStjMF0tbG1zJHZjb3ZbcixsbW1pbjErYzBdKSoxMF40CmxtZGlmMjwtKGxtcyR2Y292W3IsbG1tYXgxK2MwXS1sbXMkdmNvdltyLHBtZWRdKSoxMF40CmxtZGlmMzwtbG1kaWYxLWxtZGlmMgpkZmV2YWw8LWMocm91bmQobG1tYXgsNiksY25zbWF4LGNuc21pbixyb3VuZChsbWRpZjEsMiksY25zbWVkLHJvdW5kKGxtZGlmMiwyKSxyb3VuZChsbWRpZjMsMikpCn0KYGBgCgpEaWUgQWJow6RuZ2lna2VpdCBkZXIgc2VudGltZW50IHZhbHVlcyB2b20gVm9yaGFuZGVuc2VpbiBtdWx0aWxpbmd1YWxlciBFbGVtZW50ZSBsw6RzenQgc2ljaCBrdXJ6IHVtcmVpc3plbjogV2lyIHN0ZWxsZW4gZGVuIGdyw7ZzenRlbiBadXNhbW1lbmhhbmcgbWl0IFtjb2VmZmljaWVudF0gYGByIGdldF9sbWVyKDUsMjo0KVsxXWBgIGJlaSBgYHIgZ2V0X2xtZXIoNSwyOjQpWzJdYGAgZmVzdCwgZGllIERpZmZlcmVueiB6dSBgYHIgZ2V0X2xtZXIoNSwyOjQpWzNdYGAgYmV0csOkZ3QgYGByIGdldF9sbWVyKDUsMjo0KVs0XWBgLCB6dSBgYHIgZ2V0X2xtZXIoNSwyOjQpWzVdYGAgYGByIGdldF9sbWVyKDUsMjo0KVs2XWBgIFB1bmt0ZSwgZGVyIEFic3RhbmQgZGVyIEFiaMOkbmdpZ2tlaXQgaGllciBhbHNvIGBgciBnZXRfbG1lcig1LDI6NClbN11gYCBQdW5rdGUuICAgCgpEaWUgQWJow6RuZ2lna2VpdCBkZXIgc2VudGltZW50IHZhbHVlcyB2b24gZGVyIHR5cGUvdG9rZW4gcmF0aW8gZGVyIFRleHRlIGViZW5mYWxscyBrdXJ6IHVtcmlzc2VuOiBXaXIgc3RlbGxlbiBkZW4gZ3LDtnN6dGVuIFp1c2FtbWVuaGFuZyBtaXQgW2NvZWZmaWNpZW50XSBgYHIgZ2V0X2xtZXIoNiwyOjQpWzFdYGAgYmVpIGBgciBnZXRfbG1lcig2LDI6NClbMl1gYCBmZXN0LCBkaWUgRGlmZmVyZW56IHp1IGBgciBnZXRfbG1lcig2LDI6NClbM11gYCBiZXRyw6RndCBgYHIgZ2V0X2xtZXIoNiwyOjQpWzRdYGAsIHp1IGBgciBnZXRfbG1lcig2LDI6NClbNV1gYCBgYHIgZ2V0X2xtZXIoNiwyOjQpWzZdYGAgUHVua3RlLCBkZXIgQWJzdGFuZCBkZXIgQWJow6RuZ2lna2VpdCBoaWVyIGFsc28gYGByIGdldF9sbWVyKDYsMjo0KVs3XWBgIFB1bmt0ZS4gICAKCiMjIG5pY2UgbmV0d29yawpgYGB7ciBwbG90LW5ldCxmaWcuY2FwPSJjb29jdXJyZW5jZXMgbmV0d29yayBvZiB0ZXh0IGVsZW1lbnRzIixlY2hvPUYsd2FybmluZz1GfQpwbG90X25ldChkdGFfdCkKYGBgCiMjIGNvcnB1cyBwbGF5CkRhcyBGb2xnZW5kZSB6ZWlndCBlaW5lbiBUZXh0LCBkZW0gZWluIEFsZ29yaXRtdXMgenVncnVuZGVsaWVndCwgZGVyIHJvdWdobHkgZGllIFdhaHJzY2hlaW5saWNoa2VpdCBkZXMgVm9yaGFuZGVuc2VpbnMgZWluZXMgV29ydGVzIGFuIGRlciBqZXdlaWxpZ2VuIFBvc2l0aW9uIGltIFRleHQsIMO8YmVyIGRlbiBnZXNhbXRlbiBLb3JwdXMgYmV0cmFjaHRldCwgYmVzdGltbXQuIEVzIHRyaXR0IGFsc28gamVkZXMgV29ydCBkaWVzZXMga8O8bnN0bGljaGVuIFRleHRlcyBhbSB3YWhyc2NoZWlubGljaHN0ZW4gYW4gZGllc2VyIFN0ZWxsZSBhdWYsIHN6c2cuIGVpbiBzZWhyIHNpbXBsZXMgKnRyYW5zZm9ybWVyKiBleHBlcmltZW50LCBvaG5lIGplZ2xpY2hlIEJlcsO8Y2tzaWNodGlndW5nIHNlbWFudGlzY2gtc3ludGFrdGlzY2hlciBLYXRlZ29yaWVuIHVuZCAobm9jaCkgd2VpdCB2b24gZWluZW0gbGVybmbDpGhpZ2VuIEFsZ29yaXRobXVzIGVudGZlcm50CmBgYHtyIHAtdGV4dCwgZWNobz1GLCB3YXJuaW5nPUZBTFNFLGNhcHRpb249InRleHQgZ2VuZXJhdGVkIGJ5IHdvcmRzIHdpdGggaGlnaGVzdCBwcm9iYWJpbGl0eSBvbiBmaXhlZCBwb3NpdGlvbnMgYWxvbmcgdGV4dCBsZW5ndGgifQpwdGV4dDwtYygic2FtcGxlIiwiY29tbWVudCBpbiIsImZvciIsImZpbmFsIiwib3V0cHV0IikKcHRleHQ8LWdldF9wKHdjMykKI3RleHQ8LWNhdChwdGV4dCkKdGV4dDwtc3RyaV9qb2luKHB0ZXh0LCBjb2xsYXBzZT0iICIpCiN0ZXh0CiMgdDwtU3lzLnRpbWUoKQojIHRmPC1mb3JtYXQodCwiJWEgJWIgJWQgJVkgKCVILiVNKSIpCiMgdGNzdjwtcGFzdGUoMix0LCJybWRfZmluIixzZXAgPSAiLCIpCiMgZHQ8LWZpbGUoImRhdGVzdGFtcF9jdXJyZW50My5jc3YiLG9wZW4gPSAiYSIpCiMgd3JpdGVMaW5lcyh0Y3N2LGR0KQojIGNsb3NlKGR0KQoKYGBgCgojIyMgbW9zdCBwcm9iYWJsZSB0ZXh0CjEzNTA2LlNUOiBVbGphbmEgV29sZiAvIEdQVGVzdGVlCjw8PCAKYHIgdGV4dGAKPDw8IGZpbi4KCi0tLQoKIyBCLiBSRUY6Cg==